图形学、02 推导证明 | 任意一点经过透视投影后 z 坐标相对于之前有什么变化

齐次坐标知识点： \(\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow\begin{bmatrix} nx \\ ny \\ nz \\ n \\\end{bmatrix}\) 两个都表示同一个点

透视投影：先将远截面按一定规则缩放到跟近截面一样大，然后再正交投影

缩放规则：远截面缩放后\(z\)不变，缩放过后大小同近截面相同。

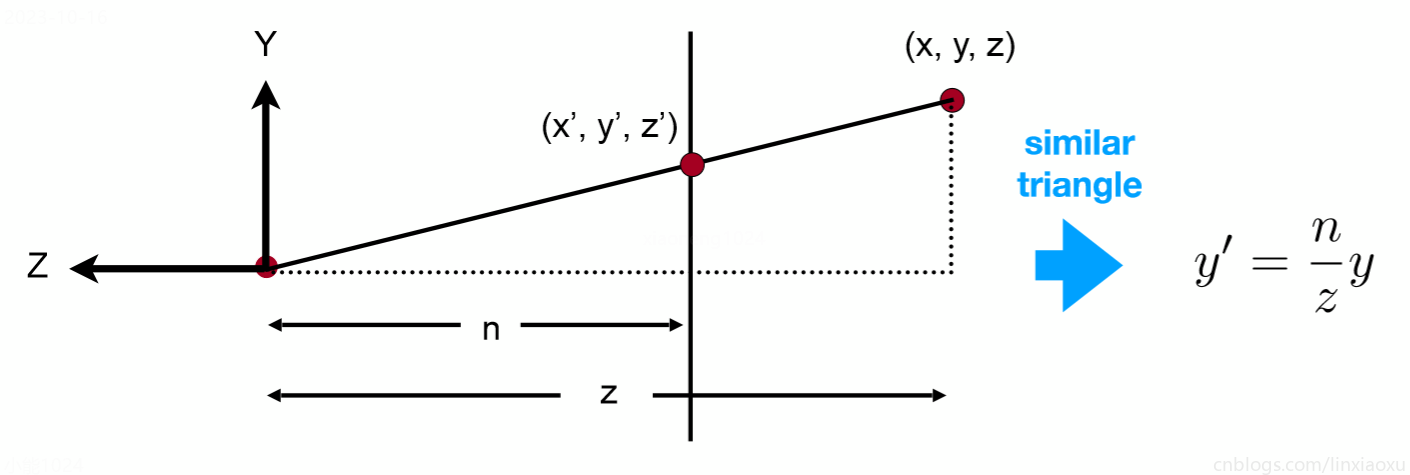
截取yz平面，\(ZNear = n,ZFar = f\) ，则任意一点经过缩放后： \(y^{’} = \frac{n}{z}y\) （相似三角形）

xz平面同理： \(x^{’} = \frac{n}{z}x\) ，即 \(\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow\begin{bmatrix} \frac{n}{z}x \\ \frac{n}{z}y \\ unknown \\ 1 \\\end{bmatrix}\Rightarrow\begin{bmatrix}nx \\ ny \\ unknown \\ z \\\end{bmatrix}\)

如此可以确定一部分矩阵参数：

\(M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ... & ... & ... & ... \\ 0 & 0 & 1 & 0 \\\end{bmatrix}\)

对于近截面和远截面上的点，透视变换后z是不变的(缩放规则)

只看第三行的结果

\(\begin{bmatrix} A&B&C&D\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow z^2\)

显然 \(A = B = 0\) ，代入 \(Z = n ，Z = f\) 有

\(Cn+D = n^{2}\)

\(Cf+D = f^{2}\)

得到 \(C = n+f,D=-nf\)

最后求得

\(M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\\end{bmatrix}\)

课后问题：对于任意一个满足 \(n\leq z\leq f\) 的点，经过透视投影后， z 坐标相对于之前有什么变化

\(M_{persp\rightarrow ortho}\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow \begin{bmatrix} nx \\ ny \\ (n+f)z-nf \\ z\\\end{bmatrix}\Rightarrow \begin{bmatrix} \frac{n}{z}x \\ \frac{n}{z}y \\ \frac{(n+f)z-nf}{z} \\ 1\\\end{bmatrix}\)

比较 \(\frac{(n+f)z-nf}{z} - z\) 跟0的关系即可，不妨乘以一个 z 得到：

\(f(z) = -z^{2} + (n+f)z-nf = (z-n)(f-z)\)

又 \(n\leq z\leq f\) ，故 \(f(z) \geq 0\) ，即透视投影后， z 坐标相对于以前离相机更远了

对 \(f(z) = \frac{(n+f)z-nf}{z} - z\) ，对 \(z\) 求偏导

\(\begin{array}{l}
\frac{\partial f}{\partial z}=\frac{(n+f) z-(n+f) z+nf}{z^{2}}-1 \\
\frac{\partial f}{\partial z}=\frac{n f}{z^{2}}-1=\frac{nf-z^{2}}{z^{2}} \\
z^{2}=nf \quad z= \pm \sqrt{nf}
\end{array}\)

\(z\) 从 \(n\) 到 \(- \sqrt{nf}\) 单调递增之后单调递减

分数求导

\(\begin{array}{l}
g(x) \neq 0 , f(x) , g(x) \text { 均可导 } \\
{\left[\frac{f(x)}{g(x)}\right]^{\prime}=\frac{f^{\prime}(x) g(x)-g^{\prime}(x) f(x)}{[g(x)]^{2}}}
\end{array}\)