【LeetCode回溯算法#04】组合总和I与组合总和II（单层处理位置去重）

组合总和

力扣题目链接(opens new window)

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：

• 输入：candidates = [2,3,6,7], target = 7,
• 所求解集为： [ [7], [2,2,3] ]

示例 2：

• 输入：candidates = [2,3,5], target = 8,
• 所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

思路

和 组合总和III 不同的点在于：

• 单个组合内元素个数没有限制，只要不超过target即可
• 由于上述原因，本题中递归的层数也没有限制

基于此，我们就不能用组合的size()作为终止条件了，并且在单层处理逻辑中，还需要使用beginIndex来确定遍历起始位置

题外话：何时需要beginIndex

如果是一个集合来求组合的话，就需要beginIndex；（例如组合、组合总和III）

如果是多个集合取组合，各个集合之间相互不影响，那么就不用beginIndex；（电话号码）

回到正题

本题的基本框架与组合总和III完全一致，下面我就写的简略一些

1、确定回溯函数参数与返回值

仍然需要定义两个数组用于保存路径值与结果

class Solution {
private:
    //定义结果变量
    vector<int> path;
    vector<vector<int>> res;
    //确定回溯函数参数与返回值
    void backtracking(vector<int>& candidates, int target, int beginIndex){

    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {

    }
};

2、确定终止条件

前面的分析提到，本题无法再使用path的大小来作为终止条件

但我们仍可以分析出需要终止的情况：

• target为0，说明已经找到满足条件的组合
• target小于0，说明过了，需要停止（在深度层面来说）

class Solution {
private:
    //定义结果变量
    vector<int> path;
    vector<vector<int>> res;
    //确定回溯函数参数与返回值
    void backtracking(vector<int>& candidates, int target, int beginIndex){
        //确定终止条件
        if(target < 0){//因为不限制单个组合中元素个数，因此递归深度也是不限的，当target < 0说明已经过了
            return;
        }
        if(target == 0){//找到目标组合
            res.push_back(path);
            return;
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {

    }
};

3、确定单层处理逻辑

这里大部分与之前的题一样，但是有个关键点是：进入下一层递归时，不要跳过当前值（即使用 i 而不是 i+1 ），因为可以在组合中出现重复值

完整代码

class Solution {
private:
    //定义结果变量
    vector<int> path;
    vector<vector<int>> res;
    //确定回溯函数参数与返回值
    void backtracking(vector<int>& candidates, int target, int beginIndex){
        //确定终止条件
        if(target < 0){//因为不限制单个组合中元素个数，因此递归深度也是不限的，当target < 0说明已经过了
            return;
        }
        if(target == 0){//找到目标组合
            res.push_back(path);
            return;
        }
        //确定单层处理逻辑
        for(int i = beginIndex; i < candidates.size(); ++i){
            //累减，满足条件时为0
            target -= candidates[i];
            path.push_back(candidates[i]);//保存路径值
            backtracking(candidates, target, i);//注意不要跳过当前值
            target += candidates[i];//回溯
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0);//从0开始
        return res;
    }
};

注意点

1、单层处理中，进入下一层递归时不要跳过当前值（并且别再的把beginIndex写到backtracking里了，应该写i才对）

2、主函数中，beginIndex应该初始化为0

组合总和II

力扣题目链接(opens new window)

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

• 示例 1:
• 输入: candidates = [10,1,2,7,6,1,5], target = 8,
• 所求解集为:

[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

• 示例 2:
• 输入: candidates = [2,5,2,1,2], target = 5,
• 所求解集为:

[
  [1,2,2],
  [5]
]

思路

与 组合总和 和 组合总和III 不同

本题提供的输入数组中，元素是有重复值的。并且仍然要求我们搜索出的组合不能有重复的

区别总结如下：

1. 本题candidates 中的每个数字在每个组合中只能使用一次。
2. 本题数组candidates的元素是有重复的，而 组合总和 是无重复元素的数组candidates

重点和难点就在于如何去重

而且就算明白了需要去重，我们还要考虑在哪去重比较合适。这时候还是需要引入树结构

（因为比较复杂懒得画了，直接用卡哥的图）

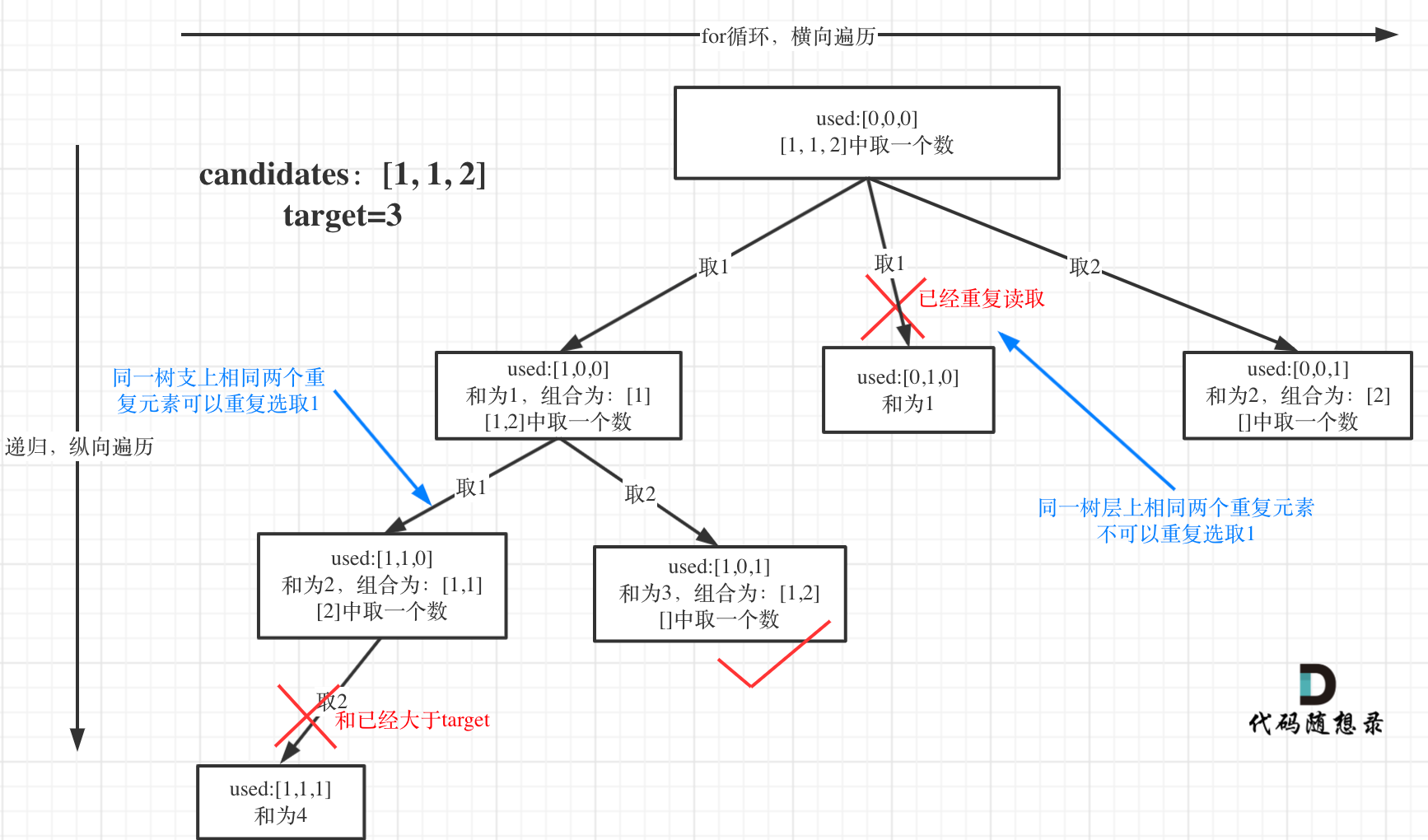
在整体结构上与之前的树基本一致

不同的是这次引入了一个used数组来标记使用过的元素

先以第一条线为例，从上往下看

第一层递归我们取[1,1,2]中的第一个1，标记used为[1,0,0]，此时组合为[1]，不满足条件

然后在第二层递归中，根据beginIndex的指向我们取[1,2]中的1，标记used为[1,1,0]。

此时组合为[1,1]，不满足条件，且再往下取就非法了

因此在第二层我们可以取[1,2]中的2，标记used为[1,0,1]。

此时组合为[1,2]，满足条件

再看第二条线，第一层递归我们取[1,1,2]中的第二个1，标记used为[0,1,0]，有没有发现问题？

因为candidates在搜索前就已经排好序，所以取第一个1的情况下回包含第二个1的所有组合

因此如果我们从第一条线搜索完毕，然后回溯到开头再从第二个1再次进入递归的话，后面搜索得到的组合一定会有重复值（与第一条线中的搜索结果重复）

例如，以第二个1开启递归的话也会得到组合[1,2]

由此我们可以发现：我们需要去重的位置应该是在单层递归时，也就是所谓的“树层”中，而在一次递归搜索的不同深度中可以使用相同的元素

上述过程中还有两个很重要的点：

1、标记数组used的状态

​ 通过used的状态可以判断是否在单层中使用了重复元素

（下面代码中再细说）

2、candidates需要提前排好序

​ 排序之后，两个重复元素会变成相邻元素。靠前的那个相邻元素的搜索结果会包含靠后那个元素的所有搜索结果

代码分析

基本框架还是一样的，就只是单层处理逻辑那不同

1、确定回溯函数的参数和返回值

输入参数不用说：candidates数组（需要先排好序）、目标值target、used数组和beginIndex

返回值不需要

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& candidates, int target, vector<bool>& used, int beginIndex){

    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {

    }
};

2、确定终止条件

和之前一样，因为这里递归深度是不限的，并且组合元素个数也是不限的

所以不可以用path的大小作为终止条件（详见 组合总和 ）

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& candidates, int target, vector<bool>& used, int beginIndex){
        //确定终止条件
        if(target < 0){
            return;
        }
        if(target == 0){
            res.push_back(path);
            return;
        }
    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {

    }
};

3、确定单层处理逻辑

在这里要去重了

首先我们要判断当前遍历的元素是否是相邻相同元素（因此candidates需要先被排序）

然后我们要判断used数组的状态

代码如下：

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& candidates, int target, vector<bool>& used, int beginIndex){
        //确定终止条件
        if(target < 0){
            return;
        }
        if(target == 0){
            res.push_back(path);
            return;
        }
        //确定单层处理逻辑
        for(int i = beginIndex; i < candidates.size(); ++i){
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
    		// used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0){
                continue;//相邻元素，且满足used[i - 1] == 0，那么之后会出现重复值，因此要跳过
            }
            target -= candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, used, i);
            //回溯
            target += candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {

    }
};

解释：

关于used[i - 1] == 0

还是拿前面那张图为例

看第一条线，used的变化是：[0,0,0]->[1,0,0]->[1,1,0]/[1,0,1]

这个过程中，没有涉及到重复的组合

第一条线结束后，回溯至最开始的位置，然后开始走第二条线

因为[1，1，2]中，两个1是相邻重复元素，所以在第二条线中used为[0,1,0]（即used[i - 1] == 0）就意味着之后会产生重复组合了（注意，必须同时满足当前元素是相邻重复元素且used[i - 1] == 0才符合可能出现重复组合的情况）

也就是说，在有两个相邻元素时（必须满足这个条件），如果used数组中出现元素1，那么1之前不能是0

例如这里第二条线还是取1，此时的i=1，并且used[i - 1] = used[0] = 0，并且确实两个相邻的1就是重复的，因此通过used可以判断出重复元素

再举一个例子，如果这里的candidates是[1，2，2]，那么当i=1，也就是选取第一个2时，此时虽然也满足used[i - 1] == 0

但是第一个2的相邻元素是1，因此不构成重复元素条件，以此类推，到第二个2时，就满足了重复条件

此时，我们需要跳过满足上述情况的遍历值

代码

在使用回溯处理数组前，一定要先对数组进行排序

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& candidates, int target, vector<bool>& used, int beginIndex){
        //确定终止条件
        if(target < 0){
            return;
        }
        if(target == 0){
            res.push_back(path);
            return;
        }
        //确定单层处理逻辑
        //注意，遍历条件还多了一个target >= 0
        for(int i = beginIndex; i < candidates.size() && target >= 0; ++i){
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
    		// used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0){
                continue;//相邻元素，且满足used[i - 1] == 0，那么之后会出现重复值，因此要跳过
            }
            target -= candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;//记录使用过当前值
            backtracking(candidates, target, used, i + 1);//跳过当前值，因为每个数字在一个组合中只能用一次（相同值的算不同的数字）
            //回溯
            used[i] = false;
            target += candidates[i];
            path.pop_back();
        }

    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		//排序
        sort(candidates.begin(), candidates.end());
        //初始化use数组
        vector<bool> used(candidates.size(), false);
        backtracking(candidates, target, used, 0);
        return res;
    }
};

注意点

1、单层处理逻辑中的for循环条件

​ 除了当前遍历的指针要在数组candidates大小范围内（i < candidates.size()），还要增加对于递归深度的约束条件，即target >= 0

​ 因为我们是通过target自减来寻找满足条件的组合的，如果target都减到小于0了，那可能非法了，也就不需要再遍历当前非法的递归层了

2、是否跳过当前值

​ 在单层处理逻辑调用递归时，如果允许在组合中出现重复元素，就不用跳过当前值

3、感觉解释得有点乱，如果再刷到有新的问题和理解再补充吧

​ TBD