Irrelevant Elements UVA-1635 （二项式定理）

vjudge链接

原题链接

乍一看似乎没什么思路，但是写几个简单的例子之后规律就变得很明显。

比如当 n=5 时，每一步计算后的结果如下：

a₁

a₁+a₂

a₁+2a₂+a₃

a₁+3a₂+3a₃+a₄

a₁+4a₂+6a₃+4a₄+a₅

显然系数“1, 4, 6, 4, 1”就是杨辉三角第五行。

故某一项的系数是否是题中 m 的倍数，就决定了最终得到的数除以 n 的余数和那一项是否有关。

二项式定理：



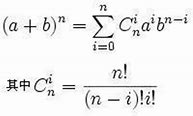
从中很容易得到前后两项的关系 C(n, k)=(n-k+1)/k*C(n, k-1) 。但是单纯用这个公式暴力得到每个系数一定会导致溢出，故需要运用唯一分解定理分别存储每个系数的素因数和指数。

一般的代码不难给出，但是一直TLE。最后发觉应该先分解 m ，再得到 m 的素因数在各个 C(n,k) 中的指数，若指数过小则可以提前结束当前的分解。由于 m>1 ，可以忽略 nk 和 n0 的情况。

我的 AC 代码如下，最初是用 ANSI C 写的，一步一步改过来，故非常不简洁。其中用 map 存储素因数，其中元素 -1 用来作为该项是否能被 m 整除的 flag。

/*
 *lang C++ 5.3.0
 *user Weilin_C
*/
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <cstdio>
#include <cmath>
#include <iostream>
#include <iomanip>
#include <algorithm>
#include <sstream>
#include <vector>
#include <map>
//#include <unordered_map>
#include <set>
#include <list>
#include <queue>
//每个数用map分质因数存储
//质数用素数筛 2-1000000000, MAXM=1000000
#define MAXM 1000000
#define MAXN 100000+5
using namespace std;
map <int, int> sta[MAXN], mm;
int pos[MAXN];
int prime[MAXM+1];
void mtomap (map<int, int> *ma, int n, int p)
{	//解码m n: 解码的数 p: 数n的个数
	int num=n;
	for (int i=2; i<=MAXM && num>0; i++) {
		if (!prime[i]) {
			while (num%i==0 && num>0) {
				num/=i;
				(*ma).insert(pair<int, int>(i, 0));
				(*ma)[i]+=p;
			}
		}
	}
	if (num>1) (*ma).insert(pair<int, int>(num, 1));
	return;
}
void ntomap (map<int, int> *ma, int n, int p)
{	//用于逐个解码第n行的杨辉三角 n: 解码的数 p: 数n的个数
    map <int, int>::iterator it;
	int num=n, t;
    if (n<2) return;
	for (it=mm.begin(); it!=mm.end(); it++) {
		t=it->first;
        if (t<2) continue;
        (*ma).insert(pair<int, int>(t, 0));
        while (num%t==0 && num>0) {
            num/=t;
            (*ma)[t]+=p;
        }
        if ((*ma)[t]<it->second) (*ma)[-1]=0;
	}
	return;
}
int judge(map<int, int> *ma)
{   //是否为0或1
    int flag=0;
    map <int, int>::iterator it;
    for (it=(*ma).begin(); it!=(*ma).end(); it++)
        if (it->second!=0 && it->first!=-1) {
            flag=1;
            break;
        }
    return flag;
}
int main()
{
    int m, n;
    //freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    /* C(n, k) = (n-k+1)/k * C(n, k-1) */
    for (int i=2; i<=sqrt(MAXM+1); i++) {
        if (prime[i]) continue;
        for (int j=i+i; j<=MAXM; j+=i) prime[j]=1;
    }
    while (scanf("%d%d", &n, &m)==2) {	//n: 杨辉三角层数
        //printf("%d %d\n", n, m);
        for (int i=0; i<=n; i++) if (!sta[i].empty()) sta[i].clear();
        mm.clear();
        sta[0][m]=0;
        sta[0][-1]=0;
        mtomap(&mm, m, 1);
        map <int, int>::iterator it;
        for (int i=1; i<n; i++) {
            for (it=sta[i-1].begin(); it!=sta[i-1].end(); it++) sta[i][it->first]=it->second;
            sta[i][-1]=1;
            ntomap(&sta[i], n-i, 1);
            ntomap(&sta[i], i, -1);
        }
        pos[0]=0;
        int ans=0;
        for (int i=0; i<n; i++) {
            if (sta[i][-1] && judge(&sta[i])) {
                ans++;
                pos[++pos[0]]=i+1;
            }
        }
        printf("%d\n", ans);
        int f=0;
        for (int i=1; i<=pos[0]; i++) {
        	if (f) putchar(' ');
            else f=1;
            printf("%d", pos[i]);
        }
        putchar('\n');
    }
    return 0;
}

by SDUST weilinfox

本文链接：https://www.cnblogs.com/weilinfox/p/12241600.html