BZOJ 3884 上帝与集合的正确用法题解

一道智慧题

其实解这题需要用到扩展欧拉定理，

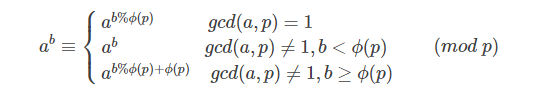
有了上面的公式，我们不难看出此题的解法。

设b为2^2^2^2^2.....显然，b要比φ（p）要大，所以可以直接套公式

modp时的答案

ans（p）=pow（2，ans（φ（p））+φ（p））%p

而边界是p=1时，ans（1）显然为0，这样递推就好了

# include<iostream>
# include<cstdio>
# include<cmath>
# include<algorithm>
const int mn = 1e7;
int phi[mn+];
int t;
long long p;
void pre()
{
    phi[]=;
    for(int i=;i<=mn;i++)
    {
        if(!phi[i])
        {
            for(int j=i;j<=mn;j+=i)
            {
               if(!phi[j])
                  phi[j]=j;
               phi[j]=phi[j]/i*(i-);
            }
        }
    }
}
long long qpow(int a,int b,int rqy)
{
    long long ans=,base=a;
    while(b)
    {
        if(b&)
            ans=ans*base%rqy;
        base=base*base%rqy;
        b>>=;
    }
    return ans;
}
long long work(long long rqy)
{
   if(rqy==)
        return ;
   return qpow(,work(phi[rqy])+phi[rqy],rqy);
}
int main()
{
    pre();
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld",&p);
        printf("%lld\n",work(p));
    }
    return ;
}