6_9 天平（UVa839）<二叉树的DFS>

前一个ubiquous通信小工具，移动只是一个由弦和电线组成的结构五彩缤纷的东西。这种移动通常被发现悬挂在小婴儿的摇篮。
图说明了一个简单的移动。它只是一个电线，悬挂的一个字符串，每一个对象的对象。它可以也被看作是一种杠杆的支点上的字符串的字符串联系的电线。从杠杆原理，我们知道，要平衡一个简单的移动的对象的重量的产品他们距离支点必须相等。这是WL×DL = WR×DR，DL是左边的距离DR是右边的距离,WL是左边的重量和WR是右边的重量。
在一个更复杂的移动的对象可能被替换由一个子移动，如下图所示。

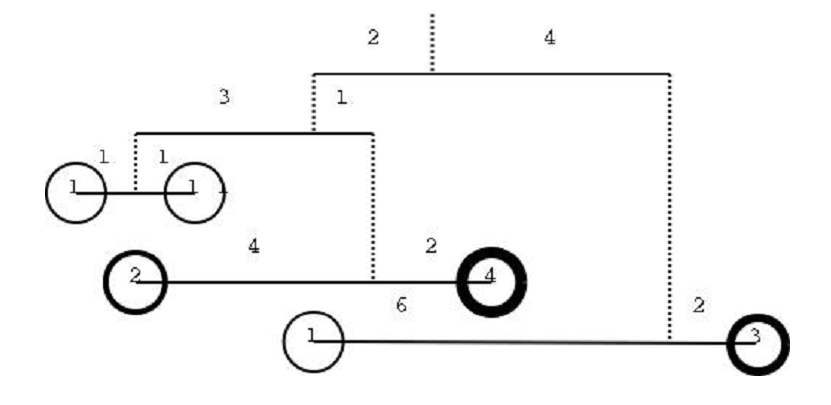
在这种情况下，如果移动是平衡的，所以我们需要你写一个程序，给定一个移动的描述作为输入，检查是否平衡。

Input

输入开始一个单独的正整数，在一行上，它指示下面的情况，每一个如下所描述的。这条线是用一个空行，还有两连续输入之间空一行。
输入由若干行组成，每一个包含4个由一个空格分隔的整数。
4个整数表示每个对象的距离和它们的权重，在格式：
WL DL WR DR
如果WL或WR是零，有一分移动挂在端和线以下定义子移动。在这种情况下，我们计算的子移动重量为其所有物体的重量的总和，无论电线串的重量。如果WL和WR是零以下行定义了两个子手机：先左后右。

Output

对于每一个测试案例，输出必须遵循下面的描述。连续两种情况下的输出将被一个空白行隔开。
如果手机处于平衡，输出“YES”，否则输出'NO'。

Sample Input
1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

Sample Output
YES