@loj - 2250@ 「ZJOI2017」仙人掌

目录

• @题目描述@
• @solution@
• @accepted code@
• @details@

---

@题目描述@

如果一个无自环无重边无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。

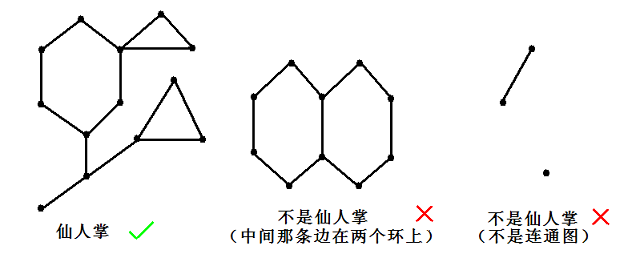
现在九条可怜手上有一张无自环无重边的无向连通图，但是她觉得这张图中的边数太少了， 所以她想要在图上连上一些新的边。同时为了方便的存储这张无向图，图中的边数又不能太多。 经过权衡，她想要加边后得到的图为一棵仙人掌。

不难发现合法的加边方案有很多，可怜想要知道总共有多少不同的加边方案。

两个加边方案是不同的当且仅当一个方案中存在一条另一个方案中没有的边。

输入格式

多组数据，第一行输入一个整数 T 表示数据组数。

每组数据第一行输入两个整数 n, m，表示图中的点数与边数。

接下来 m 行，每行两个整数 u, v(1 <= u, v <= n, u ≠ v) 表示图中的一条边。

保证输入的图联通且没有自环与重边。

输出格式

对于每组数据，输出一个整数表示方案数，当然方案数可能很大，请对 998244353 取模后输出。

样例

样例输入

2

3 2

1 2

1 3

5 4

1 2

2 3

2 4

1 5

样例输出

2

8

数据范围与提示

1 <= ∑n <= 5*10^5，1 <= ∑m <= 10^6。

@solution@

如果所有简单环都没有公共边，则一个图是仙人掌。

我们跑一遍 tarjan，将所有返祖边对应的树链标记加一。最后如果有一条边标记 > 1 则不为仙人掌。

然后初始图肯定得是一棵仙人掌。显然我们不可能跨越环连边，于是可以把所有环上的边去掉。

剩下的图变成了一棵不相交的森林。森林之间不能连边，我们只能在树上连求方案数，再把所有树的方案数相乘。

怎么求一棵树连成仙人掌的方案数？一样要求所有简单环都没有公共边，则我们相当于选出若干条没有公共边的链，求方案数。

接下来？树形 dp？貌似没有什么高效的 dp 方法。

因为没有重边，所以我们选出来的链长度 > 1。我们再把问题进一步转化：将没有被选在链中去的那些边单独作一条链，则用边不相交的链覆盖树上所有边的方案唯一对应选出若干条没有公共边的链的方案。

接着考虑每个点的贡献，设点 i 的度数为 d[i]。则我们可以将 i 连出去的边两两配对（也可以不配对），表示 i 所相邻的配对的那些边在同一条链里。

记 f[i] 表示 i 条边互相匹配的方案数，则最终答案为 f[d[i]] 之积。

f[i] 很好求，有递推式 f[i] = f[i-1] + (i-1)*f[i-2]。前者表示不匹配，后者表示选一个匹配。

@accepted code@

#include<cstdio>
#define rep(G, x) for(Graph::edge *p = G.adj[x];p;p = p->nxt)
const int MAXN = 500000;
const int MAXM = 1000000;
const int MOD = 998244353;
struct Graph{
	struct edge{
		int to; edge *nxt;
	}edges[2*MAXM + 5], *adj[MAXN + 5], *ecnt;
	void clear(int n) {
		ecnt = &edges[0];
		for(int i=1;i<=n;i++)
			adj[i] = NULL;
	}
	void addedge(int u, int v) {
		edge *p = (++ecnt);
		p->to = v, p->nxt = adj[u], adj[u] = p;
		p = (++ecnt);
		p->to = u, p->nxt = adj[v], adj[v] = p;
	}
}G1, G2;
int f[MAXN + 5];
void init() {
	f[0] = f[1] = 1;
	for(int i=2;i<=MAXN;i++)
		f[i] = (f[i - 1] + 1LL * (i - 1) * f[i - 2] % MOD) % MOD;
}
bool flag;
int d[MAXN + 5], s[MAXN + 5];
int dfn[MAXN + 5], dcnt;
void clear(int n) {
	G1.clear(n), G2.clear(n);
	for(int i=1;i<=n;i++)
		d[i] = s[i] = dfn[i] = 0;
	dcnt = 0, flag = true;
}
void tarjan(int x, int fa) {
	dfn[x] = (++dcnt);
	rep(G1, x) {
		if( p->to == fa ) continue;
		if( dfn[p->to] ) {
			if( dfn[p->to] < dfn[x] )
				s[x]++, s[p->to]--;
		}
		else tarjan(p->to, x), G2.addedge(x, p->to);
	}
}
int dfs(int x, int fa) {
	int ret = s[x];
	rep(G2, x) {
		if( p->to == fa ) continue;
		int del = dfs(p->to, x);
		ret += del;
		if( del == 0 )
			d[x]++, d[p->to]++;
		else if( del >= 2 )
			flag = false;
	}
	return ret;
}
void solve() {
	int n, m; scanf("%d%d", &n, &m), clear(n);
	for(int i=1;i<=m;i++) {
		int u, v; scanf("%d%d", &u, &v);
		G1.addedge(u, v);
	}
	tarjan(1, 0), dfs(1, 0);
	if( flag ) {
		int ans = 1;
		for(int i=1;i<=n;i++)
			ans = 1LL * ans * f[d[i]] % MOD;
		printf("%d\n", ans);
	}
	else puts("0");
}
int main() {
	init(); int T; scanf("%d", &T);
	while( T-- ) solve();
}

@details@

坚定了我对于 ZJOI 的题都是不可做的题的决心。