mysql索引原理及优化（四）

聚簇索引和非聚簇索引

分析了MySQL的索引结构的实现原理，然后我们来看看具体的存储引擎怎么实现索引结构的，MySQL中最常见的两种存储引擎分别是MyISAM和InnoDB，分别实现了非聚簇索引和聚簇索引。

聚簇索引的解释是：聚簇索引的顺序就是数据的物理存储顺序

非聚簇索引的解释是：索引顺序与数据物理排列顺序无关

（这样说起来并不好理解，让人摸不着头脑，清继续看下文，并在插图下方对上述两句话有解释）

首先要介绍几个概念，在索引的分类中，我们可以按照索引的键是否为主键来分为“主索引”和“辅助索引”，使用主键键值建立的索引称为“主索引”，其它的称为“辅助索引”。因此主索引只能有一个，辅助索引可以有很多个。

MyISAM——非聚簇索引

MyISAM存储引擎采用的是非聚簇索引，非聚簇索引的主索引和辅助索引几乎是一样的，只是主索引不允许重复，不允许空值，他们的叶子结点的key都存储指向键值对应的数据的物理地址。
非聚簇索引的数据表和索引表是分开存储的。
非聚簇索引中的数据是根据数据的插入顺序保存。因此非聚簇索引更适合单个数据的查询。插入顺序不受键值影响。
只有在MyISAM中才能使用FULLTEXT索引。(mysql5.6以后innoDB也支持全文索引)
*最开始我一直不懂既然非聚簇索引的主索引和辅助索引指向相同的内容，为什么还要辅助索引这个东西呢，后来才明白索引不就是用来查询的吗，用在那些地方呢，不就是WHERE和ORDER BY 语句后面吗，那么如果查询的条件不是主键怎么办呢，这个时候就需要辅助索引了。

InnoDB——聚簇索引

聚簇索引的主索引的叶子结点存储的是键值对应的数据本身，辅助索引的叶子结点存储的是键值对应的数据的主键的键值。因此主键的值长度越小越好，类型越简单越好。
聚簇索引的数据和主键索引存储在一起。
聚簇索引的数据是根据主键的顺序保存。因此适合按主键索引的区间查找，可以有更少的磁盘I/O，加快查询速度。但是也是因为这个原因，聚簇索引的插入顺序最好按照主键单调的顺序插入，否则会频繁的引起页分裂，严重影响性能。
在InnoDB中，如果只需要查找索引的列，就尽量不要加入其它的列，这样会提高查询效率。

*使用主索引的时候，更适合使用聚簇索引，因为聚簇索引只需要查找一次，而非聚簇索引在查到数据的地址后，还要进行一次I/O查找数据。

*因为聚簇辅助索引存储的是主键的键值，因此可以在数据行移动或者页分裂的时候降低成本，因为这时不用维护辅助索引。但是由于主索引存储的是数据本身，因此聚簇索引会占用更多的空间。

*聚簇索引在插入新数据的时候比非聚簇索引慢很多，因为插入新数据时需要检测主键是否重复，这需要遍历主索引的所有叶节点，而非聚簇索引的叶节点保存的是数据地址，占用空间少，因此分布集中，查询的时候I/O更少，但聚簇索引的主索引中存储的是数据本身，数据占用空间大，分布范围更大，可能占用好多的扇区，因此需要更多次I/O才能遍历完毕。

下图可以形象的说明聚簇索引和非聚簇索引的区别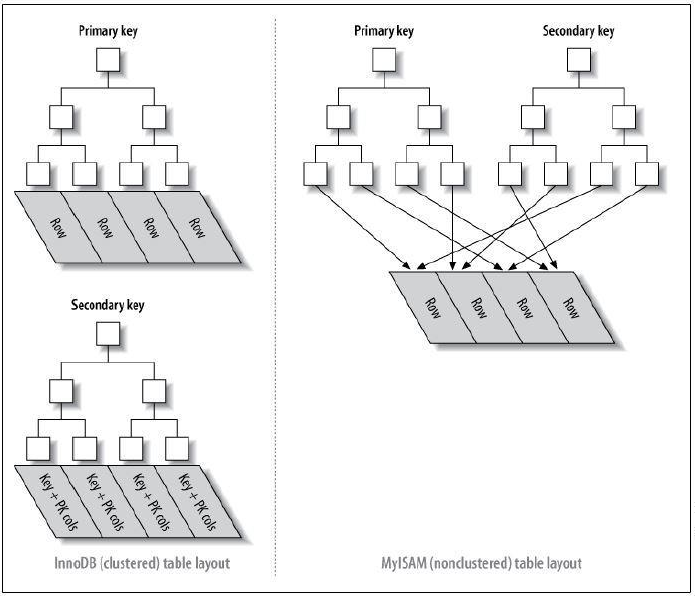

从上图中可以看到聚簇索引的辅助索引的叶子节点的data存储的是主键的值，主索引的叶子节点的data存储的是数据本身，也就是说数据和索引存储在一起，并且索引查询到的地方就是数据（data）本身，那么索引的顺序和数据本身的顺序就是相同的；

而非聚簇索引的主索引和辅助索引的叶子节点的data都是存储的数据的物理地址，也就是说索引和数据并不是存储在一起的，数据的顺序和索引的顺序并没有任何关系，也就是索引顺序与数据物理排列顺序无关。

此外MyISAM和innoDB的区别总结如下：

总结如下：

InnoDB 支持事务，支持行级别锁定，支持 B-tree、Full-text 等索引，不支持 Hash 索引；
MyISAM 不支持事务，支持表级别锁定，支持 B-tree、Full-text 等索引，不支持 Hash 索引；
此外，Memory 不支持事务，支持表级别锁定，支持 B-tree、Hash 等索引，不支持 Full-text 索引；

原文链接：https://blog.csdn.net/tongdanping/article/details/79878302