AR模型与数据平稳性之间的关系

作者：桂。

时间：2017-12-19  21:39:08

链接：http://www.cnblogs.com/xingshansi/p/8068021.html

---

前言

　　前几天碰到一个序列分析的问题，涉及到自回归（auto-regression, AR）等模型，但如何确定序列的平稳性呢？ 发现金融数据分析里，这方面的知识很多，以后用到可以借鉴，例如伍德里奇《计量经济学导论》，高铁梅《计量经济分析方法与建模》，关键词：序列检测与判定、概率模型、统计。

一、平稳特性

序列的平稳特性通常从三个方面分析：

1）均值

均值不应该是关于时间t的函数，而应该是一个常数。

2）方差

方差不应该是时间的函数，即方差需要有：同方差性（homoscedasticity）

3）协方差

i时刻与i+m时刻协方差不应该是时间的函数：

常用的平稳定义包括：1）严平稳；2）宽平稳；对于手中的序列，严平稳难以判定，通常用宽平稳判据：一阶矩、二阶矩，即从均值、方差角度考虑，而不再考虑高阶分布特性。

给定序列：

X(t) = Er(t)

其中Er(t)为高斯白噪声序列，则x(t)为平稳信号。

给定序列：

X(t) = X(t-1) + Er(t)

这便是随机游走：

小女孩从初始位置出发，经过若干步之后，位置可表示为：

X(t) = X(0) + Sum(Er(1),Er(2),Er(3).....Er(t))

随机游走的平稳性:

1）均值

E[X(t)] = E[X(0)] + Sum(E[Er(1)],E[Er(2)],E[Er(3)].....E[Er(t)])

均值是常数。

2）方差

Var[X(t)] = Var[X(0)] + Sum(Var[Er(1)],Var[Er(2)],Var[Er(3)].....Var[Er(t)])

即

Var[X(t)] = t * Var(Error) = Time dependent.

方差是时间的函数，可见随机游走是非平稳过程。

二、平稳性检验

上文分析随机游走：

X(t) = X(t-1) + Er(t)

是非平稳过程。

白噪声序列：

X(t) = Er(t)

是平稳随机过程。

现在进行折中：

X(t) = Rho * X(t-1) + Er(t)

上面两个例子分别对应Rho = 0、1.

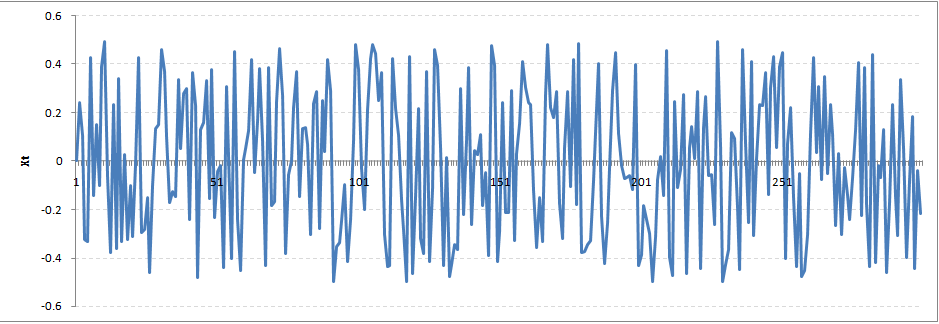
Rho = 0:

Rho= 0.5:

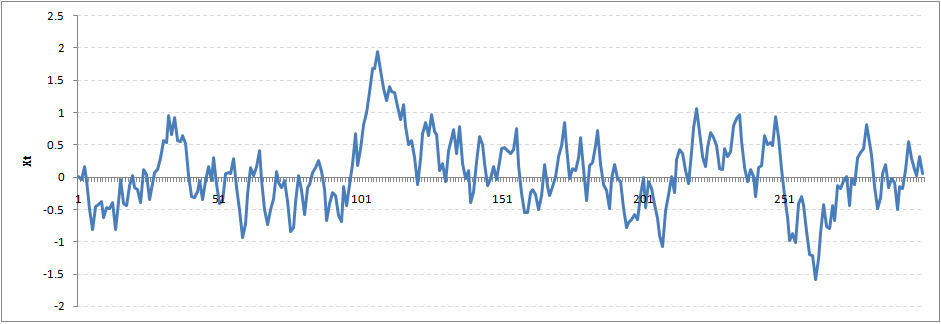
Rho = 0.9:

Rho = 1:

从图中可以看出，除了Rho = 1具有明显的非平稳特性外，其余序列都可近似看作平稳特性，此时已经不是严格意义的平稳（不一定满足宽平稳条件），通常借助其他方式检验：

H0:...; H1:...，进行判定。

三、其它

对于AR模型：

先看AR（1）的情形：

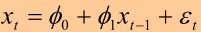
求方差：

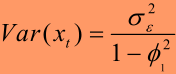
可以看出平稳条件：，这与上文Rho绝对值介于（0，1）的结论是一致的。

推广到AR（2）:

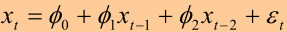
平稳条件为对应特征方程（高数-齐次方程的内容）：

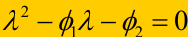
即：

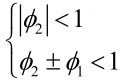
更一般地，对于AR模型：特征值均论在单位圆内。可以看出平稳的判定是一种思路，与平稳条件：宽平稳并非严格等价。但这提供了检验平稳性的思路。ARMA等模型的分析与此类似，AR、ARMA的模型要求序列满足平稳特性，但对于拟合残差没有任何约束，基于异方差特性的ARCH等模型就是从这个种子里生出的新芽。