[leetcode]149. Max Points on a Line多点共线

Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.

Example 1:

Input: [[1,1],[2,2],[3,3]]
Output: 3
Explanation:
^
|
|        o
|     o
|  o
+------------->
0  1  2  3  4

Example 2:

Input: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4
Explanation:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

题意：

给定二维平面上一些点，问最多多少个点共线

Solution1: HashMap

解本题需要的背景知识：【Math Fact】All the points in a line share the same slop.

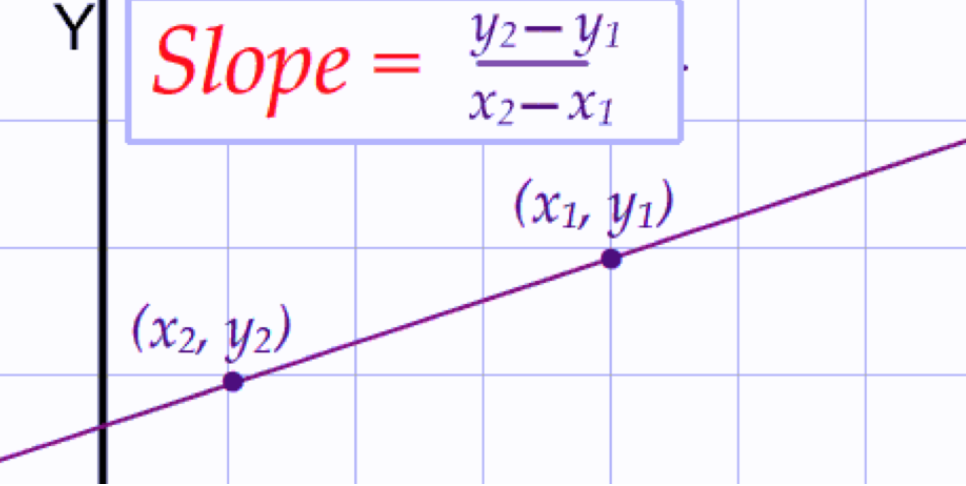
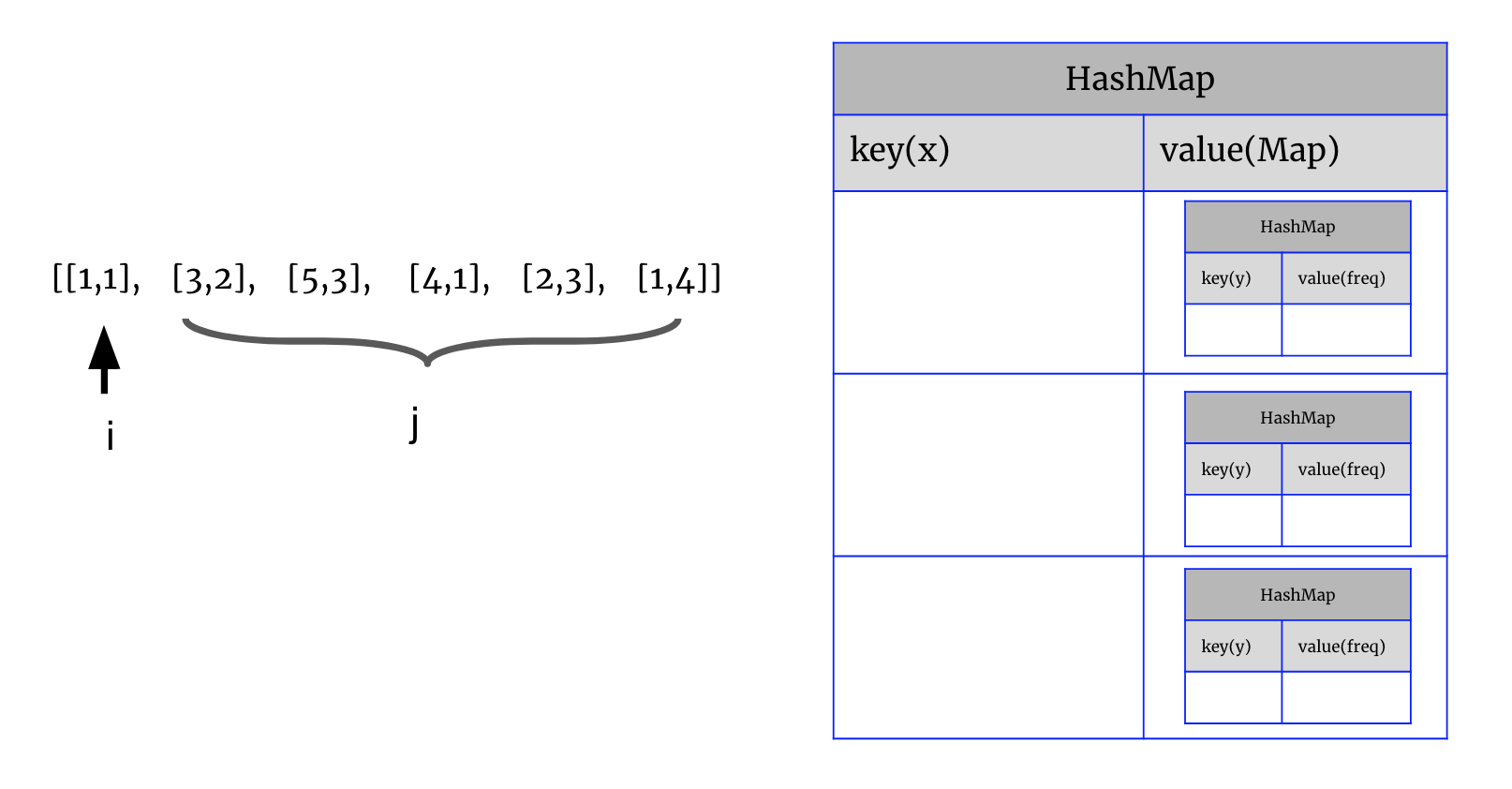
The question is like standing at points[i],  find max number of points in points[j], such that points[i] and points[j] are on the same line.

1. If points[i], points[j] 's coordinator are the same, they are overlapping.

2. Otherwise, they are nonoverlapping. Based on the fact that "All the points in a line share the same slop", we use the greatest common divisor(最大公约数) to get the lowest term(最简化) for points[i], points[j]'s coordinator.  即[2,4] 和[4,8]， 我们用求最大公约数的方式，将其斜率化成最简形式： 1/2 和 1/2

3. We use Map<x, Map<y, occurance>> map to get such slop from x and y's occurance. Then we know how many non-overlapping points in such line.

code

 public class MaxPointsonaLine {
     // 已经给定的Point class
     class Point {
         int x;
         int y;

         Point() {
             x = 0;
             y = 0;
         }

         Point(int a, int b) {
             x = a;
             y = b;
         }
     }

     public int maxPoints(Point[] points) {
         int result = 0;
         Map<Integer, Map<Integer, Integer>> map = new HashMap<>();
         // standing at points[i]
         for (int i = 0; i < points.length; i++) {
             map.clear();
             int overlapping = 0;
             int nonoverlapping = 0;
             // checking points[j]
             for (int j = i + 1; j < points.length; j++) {
                 int x = points[j].x - points[i].x;
                 int y = points[j].y - points[i].y;
                 if (x == 0 && y == 0) {
                     overlapping++;
                     continue;
                 }
                 int gcd = generateGCD(x, y);
                 if (gcd != 0) {
                     x = x / gcd;
                     y = y / gcd;
                 }
                 if (map.containsKey(x)) {
                     if (map.get(x).containsKey(y)) {
                         map.get(x).put(y, map.get(x).get(y) + 1);
                     } else {
                         map.get(x).put(y, 1);
                     }
                 } else {
                     Map<Integer, Integer> m = new HashMap<>();
                     m.put(y, 1);
                     map.put(x, m);
                 }
                 overlapping = Math.max(nonoverlapping, map.get(x).get(y));
             }
             result = Math.max(result, overlapping + nonoverlapping + 1);
         }
         return result;
     }

     public int generateGCD(int a, int b) {
         return (b == 0) ? a : generateGCD(b, a % b);
     }
 }