[matlab] 21.灰色预测、线性回归分析模型与最小二乘回归 (转载)

灰色预测的主要特点是只需要4个数据,就能解决历史数据少,序列的完整性以及可靠性低的问题,能将无规律的原始数据进行生成得到规律性较强的生成序列,易于检验

但缺点是只适合中短期的预测,且只适合指数级增长的预测.

在建立灰色预测模型之前，需先对原始时间序列进行数据处理，经过数据预处理后的数据序列称为生成列。对原始数据进行预处理，不是寻找它的统计规律和概率分布，而是将杂乱无章的原始数据列通过一定的方法处理，变成有规律的时间序列数据，即以数找数的规律，再建立动态模型。

灰色预测通过鉴别系统因素之间发展趋势的相异程度，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物的未来发展趋势

步骤

1. 对原始数据进行累加
2. 构造累加矩阵 BB 与常数向量
3. 求解灰参数
4. 将参数带入预测模型进行数据预测

例

已知某公司 1999——2008 年的利润为（单位：元/年）：[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670]，现在要预测该公司未来几年的利润情况

clear
syms a b;
c=[a b]';
A=[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670];
B=cumsum(A);  % 原始数据累加
n=length(A);
for i=1:(n-1)
    C(i)=(B(i)+B(i+1))/2;  % 生成累加矩阵
end
% 计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
% 预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
    F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a ;
end
G=[];G(1)=A(1);
for i=2:(n+10)
    G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1999:2008;
t2=1999:2018;
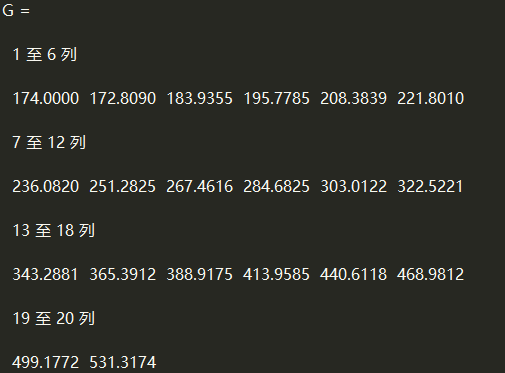
G
plot(t1,A,'k>',t2,G)  %原始数据与预测数据的比较
xlabel('年份')
ylabel('利润')

灰色预测

例: 江水质的预测

对原题附件 4 中的数据进行整理可得表如下：

clear
syms a b;
c=[a b]';
A=[174 179 183 189 207 234 220.5 256 270 285];
B=cumsum(A);  % 原始数据累加
n=length(A);
for i=1:(n-1)
    C(i)=(B(i)+B(i+1))/2;  % 生成累加矩阵
end
% 计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
% 预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
    F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a ;
end
G=[];G(1)=A(1);
for i=2:(n+10)
    G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1995:2004;
t2=1995:2014;
G
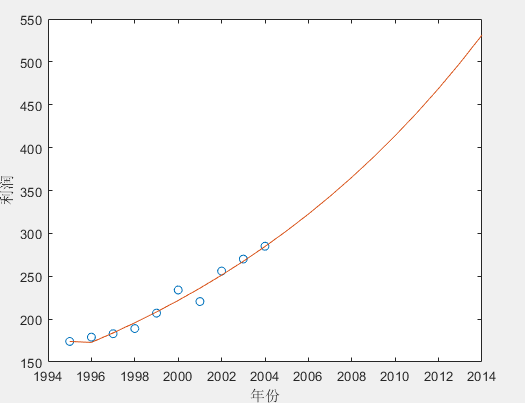
plot(t1,A,'o',t2,G)  %原始数据与预测数据的比较
xlabel('年份')
ylabel('利润')

灰色预测

例. 一元线性回归分析模型

X = [80;110;160;230;300];
Y = [4600;5500;5850;5350;6200];
XX = [ones(5,1),X];  % 为了在回归得到常数项系数 a，将 XX 作为回归的自变量
C =regress(Y,XX)   % C 是一个回归系数矩阵

一元线性回归分析模型

根据下表预测 2011 年产量为 320 万件时的总成本

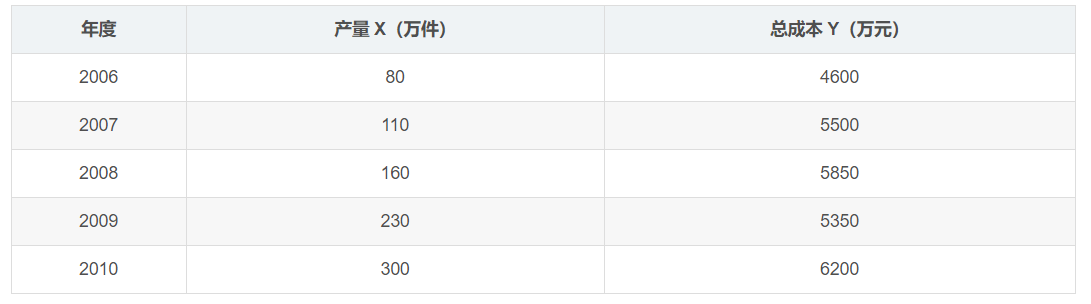
假设成本 Y 是产量 X 的一次线性函数，即二者的关系是：Y = a + b*X

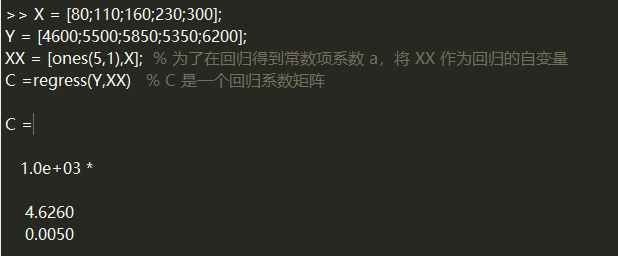
因此，可以认为产量与成本的关系为：Y = 4626.0 + 5.0 * X。 
当 X = 320 万件时，Y = 6226（万元）

clc, clear all;

x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];

figure
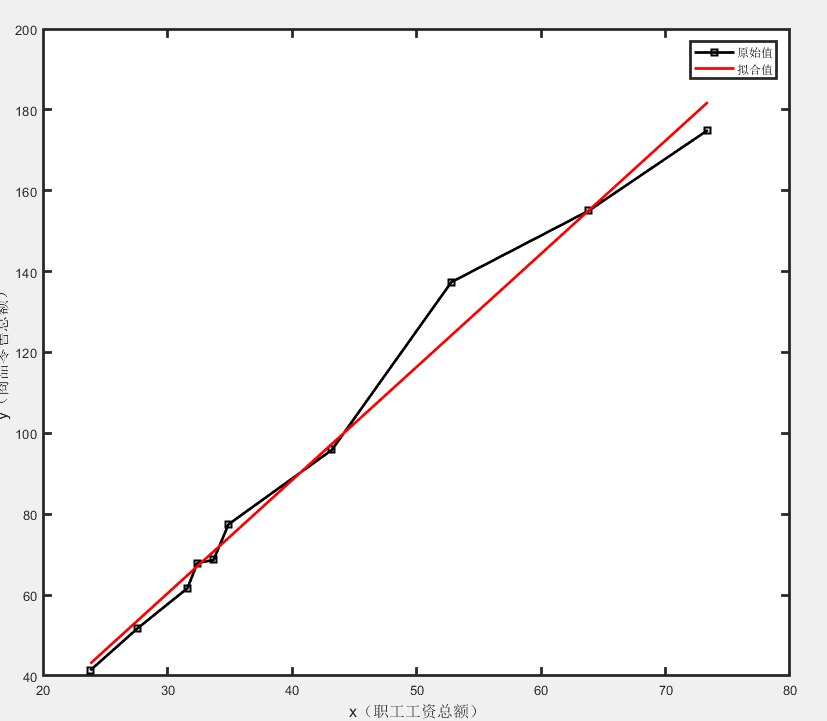
plot(x,y,'k*-','linewidth',2)                         %作散点图

xlabel('x（职工工资总额）','fontsize', 12)           %横坐标名
ylabel('y（商品零售总额）', 'fontsize',12)           %纵坐标名
set(gca,'linewidth',2);

% 采用最小二乘拟合
Lxx=sum((x-mean(x)).^2);
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0;
hold on
plot(x, y1,'r','linewidth',2);
legend('原始值','拟合值')

最小二乘回归

在用最小二乘回归之前，先绘制了数据的散点图，这样就可以从图形上判断这些数据是否近似成线性关系。当发现它们的确近似在一条线上后，再用线性回归的方法进行回归，这样也更符合我们分析数据的一般思路。

更多详细具体参考 回归方法

MATLAB连续模型求解方法 微分方程

元胞自动机

评价型模型求解方法

数学建模之机器学习