我们在学习期间都接触过自然常数e，也知道e ≈ 2.718，学过极限的同学应该也知道

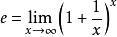
那么大家知道e的含义是什么吗？为啥叫“自然常数”？

e的含义可以用一个计算利息的例子来解释。

假如你有1块钱，银行抽风了一年利率100%。

如果一年结算一次，一年后就能得到1×(1+1)=2块钱。

如果半年结算一次，上半年的计息计入下半年的本金，一年后就能得到1×(1+0.5)×(1+0.5)=1×(1+0.5)=2.25块钱。这样就多出了两毛五。

如果像余额宝一样，每天都结算利息，那么一年后你就能得到

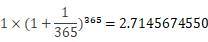
比最开始多了七毛多。

那么，如果每一秒结算一次，或者每一毫秒结算一次，或者每过无穷短的时间结算一次。那么钱岂不是可以一直加下去？

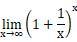
答案是否定的，这其实就又回到了最开始的那个式子，它的结果是一个常数，约等于2.71828182845904523536，也就是e。

如果不能理解的话想一想为什么下面无穷个正数相加却等于一个常数

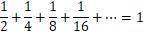
综上，e的含义可以理解为增长的极限，“自然常数”的“自然”也可以理解为它是非人为的，我们只是发现了它。就像圆周率π一样，它也存在于生活的很多地方。

原文：https://baijiahao.baidu.com/s?id=1592672728768901992&wfr=spider&for=pc

我们数学中常用的自然常数e代表什么？看完长知识了！的更多相关文章

  1. PHP中的__call和__callStatic方法（未看完）

    如何防止调用不存在的方法而出错,使用__call魔术重载方法. __call方法原型如下: mixed __call(string $name,array $arguments) 当调用一个不可访问的 ...

  2. iOS开发中常用的数学函数

    iOS开发中常用的数学函数 /*---- 常用数学公式 ----*/ //指数运算 3^2 3^3 NSLog(,)); //result 9 NSLog(,)); //result 27 //开平方 ...

  3. JAVA项目中常用的异常处理情况总结

    JAVA项目中常用的异常知识点总结 1. java.lang.nullpointerexception这个异常大家肯定都经常遇到,异常的解释是"程序遇上了空指针",简单地说就是调用 ...

  4. JAVA项目中常用的异常知识点总结

    JAVA项目中常用的异常知识点总结 1. java.lang.nullpointerexception这个异常大家肯定都经常遇到,异常的解释是"程序遇上了空指针",简单地说就是调用 ...

  5. C语言中math.h中常用的函数

    1.绝对值 ①函数原型: int abs(int x); 函数功能: 求整数x的绝对值 int number=-1234; abs(number); ②函数原型:double fabs(double ...

  6. 自然常数e的含义

    e是一个重要的常数,但是它的直观含义却不像 π 那么明了.我们都知道,圆的周长与直径之比是一个常数,这个常数被称为圆周率,记作 π = 3.14159......可是e代表什么呢? e是“指数”(ex ...

  7. JDK库rt包中常用包说明

    日常开发中的api都在rt包中,具体路径为:/jdk1.8.0_162/jre/lib中,注意是在jre中. 每个包中大致包含以下几个部分: 接口 类 枚举 异常 错误 注解 J2EE开发中常用的包 ...

  8. 自然常数e的由来以及计算机为什么是二进制

    背景 ​ 昨晚我在看一本书,叫<数学极客>,看到第六章<e:不自然的自然数>,这个数最早开始接触应该是高一的时候,那时候问老师,这个数是怎么来的,老实说,和圆周率一样,是一个常 ...

  9. 网页中常用HTML字符实体

    摘要: 一些字符在 HTML 中拥有特殊的含义,比如小于号 () 用于定义 HTML 标签的开始.如果我们希望浏览器正确地显示这些字符,我们必须在 HTML 源码中插入字符实体. 字符实体有三部分:一 ...

随机推荐

  1. Ajax 调用的WCF

    支持ajax 跨域调用的WCF搭建 1.新建一个"ASP.NET空Web应用程序"项目. 2.新建一个“WCF服务(支持ajax)”. 3.修改WCFAjaxService.svc ...

  2. poj-3080(kmp+暴力枚举)

    题意:给你多个字符串,问你这几个字符串的最长公共子串是哪个,如果有多个,输出字典序最大的那个,如果最长的公共子串长度小于3,输出一个奇怪的东西: 解题思路:首先看数据,数据不大,开始简单快乐的暴力之路 ...

  3. Nginx upstream变量

    log_format varups '$upstream_addr $upstream_connect_time $upstream_header_time $upstream_response_ti ...

  4. JarvisOJ Basic easyRSA

    还记得veryeasy RSA吗?是不是不难?那继续来看看这题吧,这题也不难. 已知一段RSA加密的信息为:0xdc2eeeb2782c且已知加密所用的公钥: (N=322831561921859 e ...

  5. Hibernate查询以及优化策略04

    一. HQL查询 1. HQL(hibernate query language)单表查询 1.1 准备项目 创建项目: hinernate-03-query 引入jar,同前一个项目 复制实体(订单 ...

  6. Matplotlib学习---用matplotlib画直方图/密度图（histogram, density plot）

    直方图用于展示数据的分布情况,x轴是一个连续变量,y轴是该变量的频次. 下面利用Nathan Yau所著的<鲜活的数据:数据可视化指南>一书中的数据,学习画图. 数据地址:http://d ...

  7. JeeSite 部署到linux服务器

    1.打包 改数据库连接 打包war包https://www.cnblogs.com/wdw31210/p/9878422.html 2.上传到linux 服务器的tomcat/webapps/ 下 安 ...

  8. MT【285】含参数函数绝对值的最大值

    (浙江2013高考压轴题)已知$a\in R$,函数$f(x)=x^3-3x^2+3ax-3a+3$(2)当$x\in[0,2]$时,求$|f(x)|$的最大值. 分析:由题意$f^{'}(x)=3x ...

  9. 清理XFCE4卸载残留

    apt-get remove xfce4 apt-get remove xfce4* apt-get autoremove apt-get autoclean apt-get clean --- 更新 ...

  10. python学习day6 数据类型Ⅳ(集合)

    day6 数据类型-集合 内容补充: 列表功能: .reverse()反转 v = [1,2,3,4,5,6]v.reverse()print() #[6, 5, 4, 3, 2, 1] .sort( ...