洛谷P1038神经网络题解

题目

因此我们先分析一下题目的坑点。

1：

题目的图分为输入层，输出层，以及中间层。

我们怎么判断呢？？？可以判断每个点的入度及出度。如果一个点的入度为零则它是输入层，出度为零则是输出层。其余情况便是中间层。

因为根据原题所描述的

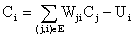公式中的 Wji​ （可能为负值）表示连接 j 号神经元和 i 号神经元的边的权值。

当 C_i 大于 0 时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为 C_i​。

我们可以得出只有一个点是终点时，才会满足上述公式，或者说是（非输入层），因此我们可以想到如果想让一个中间层或输出层的状态确定，那么与他相连的边的C_j值都要乘上，如果有一条不乘上，就不满足。

很容易想到现在所有的Cj的值必须是已经算出来的了。

因此我们可以想到拓扑排序，因为拓扑排序的条件就是这个点与他相连的边的起点都要先完成他们的任务。

2：

根据上文所知，C值一开始是不确定的，所以我们可以新建一个now数组，来表示现在这个点的状态值，当他相连边的起点都加到now的值上时，即入度为0，那此时的now值就是他的状态值。

但是这里有一个大坑点：只有这条边的起点的C值>0时才可以加上。

并且你不能在刚取出这个起点的时候就判断（别问我怎么知道的）。

因为如果你判断了，那终点的入度就减不了了。

用拓扑排序的套路，把这个点入队。再反复进行上面的几步。

分析完这个题的坑点，基本上这个题就解决了。

代码：

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
queue<int>q;
int n,m,in_degree[],out_degree[];
bool flag;
int tot,lin[];
int c[],u[],now[];//now是现在的状态值，并不是最终的。
struct cym {
    int from,to,next,len;
} e[];
void add(int x,int y,int v)
{
    e[++tot].from=x;
    e[tot].to=y;
    e[tot].len=v;
    e[tot].next=lin[x];
    lin[x]=tot;
    in_degree[y]++;//判断是否是输出层和输入层及拓扑排序
    out_degree[x]++;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=; i<=n; i++)
        scanf("%d%d",&c[i],&u[i]);
    for(int i=; i<=m; i++) {
        int x,y,v;
        scanf("%d%d%d",&x,&y,&v);
        add(x,y,v);
    }
    for(int i=; i<=n; i++)
        if(!in_degree[i])//如果这个点是输入层他的状态是最先确定的，因此根据FIFO原则，用队列优化，也是拓扑排序的方法。
            q.push(i);
    while(!q.empty()) {
        int cur=q.front();
        q.pop();
        //if(c[cur]<=0)加上这两句是不行的，因为要减去下文的入度
        //continue;
        for(int i=lin[cur]; i; i=e[i].next)
        {
            in_degree[e[i].to]--;
            if(c[e[i].from]>)//判断该点是否可以向下传递
            now[e[i].to]+=c[e[i].from]*e[i].len;
            if(!in_degree[e[i].to])//当入度为零时说明所有先决条件都已满足，满足拓扑排序，可以入队
            {
                now[e[i].to]-=u[e[i].to];//别忘了减去阈值
                c[e[i].to]=now[e[i].to];
                q.push(e[i].to);
            }
        }
    }
    for(int i=; i<=n; i++)
        if(out_degree[i]==&&c[i]>)//判断是否为输出层且最后状态>0
        {
            flag=;
            printf("%d %d\n",i,c[i]);
        }
    if(!flag)
        printf("NULL");
}