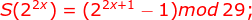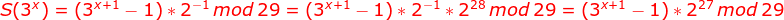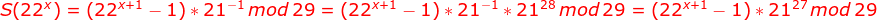HDU 1452 Happy 2004(因数和+费马小定理+积性函数)
Happy 2004
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2183 Accepted Submission(s): 1582
Problem Description
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).
Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.
Input
The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000).
A test case of X = 0 indicates the end of input, and should not be processed.
Output
For each test case, in a separate line, please output the result of S modulo 29.
Sample Input
1
10000
0
Sample Output
6
10
Source
ACM暑期集训队练习赛(六)
Recommend
lcy | We have carefully selected several similar problems for you: 1695 1788 1060 1370 1211
题解:
1.积性函数:函数f如果满足对于任意两个互质的正整数m和n,均有f(mn)=f(m)f(n),就称f为积性函数(或乘性函数)。如果对于任意两个正整数m和n,均有f(mn)=f(m)f(n),就称为完全积性函数。
2.因数和函数:
3.因数和函数为积性函数,结合费马小定理:
#include<iostream>
using namespace std;
int mul(int a,int x){
int ans=1;
while(x){
if(x&1)
ans=a*ans%29;
x>>=1;
a=a*a%29;
}
return ans;
}
int main()
{
int x;
while(~scanf("%d",&x)&&x)
{
int ans1=(mul(2,2*x+1)-1)%29;
int ans2=(mul(3,x+1)-1)%29*mul(2,27)%29;
int ans3=(mul(22,x+1)-1)%29*mul(21,27)%29;
printf("%d\n",ans1*ans2*ans3%29);
}
return 0;
}
HDU 1452 Happy 2004(因数和+费马小定理+积性函数)的更多相关文章
- HDU 5667 Sequence 矩阵快速幂+费马小定理
题目不难懂.式子是一个递推式,并且不难发现f[n]都是a的整数次幂.(f[1]=a0;f[2]=ab;f[3]=ab*f[2]c*f[1]...) 我们先只看指数部分,设h[n]. 则 h[1]=0; ...
- 2014多校第一场 I 题 || HDU 4869 Turn the pokers(费马小定理+快速幂模)
题目链接 题意 : m张牌,可以翻n次,每次翻xi张牌,问最后能得到多少种形态. 思路 :0定义为反面,1定义为正面,(一开始都是反), 对于每次翻牌操作,我们定义两个边界lb,rb,代表每次中1最少 ...
- hdu 4869 Turn the pokers(组合数+费马小定理)
Problem Description During summer vacation,Alice stay at home for a long time, with nothing to do. S ...
- HDU——5667Sequence(矩阵快速幂+费马小定理应用)
Sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total S ...
- HDU 4704 Sum (高精度+快速幂+费马小定理+二项式定理)
Sum Time Limit:1000MS Memory Limit:131072KB 64bit IO Format:%I64d & %I64u Submit Status ...
- 数学--数论--HDU 1098 Ignatius's puzzle (费马小定理+打表)
Ignatius's puzzle Problem Description Ignatius is poor at math,he falls across a puzzle problem,so h ...
- 数论初步(费马小定理) - Happy 2004
Description Consider a positive integer X,and let S be the sum of all positive integer divisors of 2 ...
- 数论 --- 费马小定理 + 快速幂 HDU 4704 Sum
Sum Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=4704 Mean: 给定一个大整数N,求1到N中每个数的因式分解个数的 ...
- HDU 4704 Sum(隔板原理+组合数求和公式+费马小定理+快速幂)
题目传送:http://acm.hdu.edu.cn/showproblem.php?pid=4704 Problem Description Sample Input 2 Sample Outp ...
随机推荐
- C# 事务 四种事务隔离级别
http://www.zsythink.net/archives/1233 不同隔离级别的问题 脏读(Dirty Read) 一个事务处理过程里读取了另一个未提交的事务中的数据 例子: 当一个事务 ...
- Hibernate的学习(二)
---恢复内容开始--- 一.多表的建表原则 1.一对多的关系:例如 一个客户有多个联系人: 表与表一对多的关系:在一对多时,多的表中添加一个外键,用来和一的表的主键.产生联系. 2.多对多的关系:例 ...
- Vue -自定义指令&钩子函数
除了核心功能默认内置的指令,Vue也允许注册自定义指令 页面加载后,让文本框自动获取焦点,原生js做法是获取文本框元素后调用focus()方法,但Vue不建议手动操作DOM元素,所以此时要自定义指令 ...
- 使用SpringSocial开发微信登录
⒈编写微信用户对应的数据结构 package cn.coreqi.social.weixin.entities; /** * 微信用户实体类 */ public class WeixinUserInf ...
- 代码学习-Linux内核网卡收包过程(NAPI)【转】
转自:https://blog.csdn.net/crazycoder8848/article/details/46333761 版权声明:本文没有任何版权限制,任何人可以以任何方式使用本文. htt ...
- TextArea 保存时换行符处理
后台数据保存时就要处理“\r\n",替换成”<br />",前台(html)页面显示时再做下处理. 自己是mvc页面,用到了两个方法:Html.Raw(),以及Http ...
- HttpResonse 要记得关闭
写了一个小程序,要识别网站上的图片,用到HttpRequest发请求,HttpResponse接受返回数据.刚开始循环可以跑两个,但是总是提示超时.后来查资料发现,在Http协议中,规定了同个Http ...
- hibernate框架学习之二级缓存(测试用例)
HqlDemoApp.java package cn.itcast.h3.query.hql; import java.io.Serializable; import org.hibernate.Qu ...
- 004_wireshark专题
一.常用的wireshark搜索语法 (1) http.request.uri contains "admin/activities" #搜索URL包含"admin/ac ...
- java的小数比较反例
double num = 0.3; System.out.println(num); System.out.println(num - 0.2); System.out.println(num - 0 ...