C温故补缺(六):C反汇编常用的AT&Tx86语法

C语言反汇编用到的AT&T x86汇编语法

默认gcc -S汇编出的,以及反汇编出的,都是AT&T x86代码,可以用-masm=intel指定为intel x86汇编格式

gcc -S test.c -masm=intel -o test.s

有时编译器会自动优化汇编代码,导致得到的汇编与源程序不对应,可以用-O0参数关闭优化

gcc -S test.c -O0 -o test.s

指令的长度后缀

AT&T语法要求在指令后面加上后缀表示长度,根据操作的是1字节,2字节,4字节,8字节,分别对应后缀b,w,l,q,即byte(1字节),word(1个字),long word(双字),quad word(四字)

跳转和函数调用指令的语法

寄存器:跳转到寄存器%rax内容对应的地址,不是jmpq %rax,而是jmpq *%rax
立即数:直接跳,不用加*号
内存:如果想跳到%rip+0x10内存对应的地址,用jmpq *0x10(%rip)

指令寄存器相对寻址(%rip-relative)

在x86_64汇编中,可以使用指令寄存器IP相对寻址这种方式来定位全局变量和函数

如:

static int i;

int f(){

    i=i+4;

    return i;

}

    movl    i(%rip), %eax

    addl    $4, %eax

    movl    %eax, i(%rip)

    movl    i(%rip), %eax

就是通过%rip寻址的

各个section

.test:存放代码对应的指令
.bss:存放未初始化的全局和静态变量,在运行时该区域初始全是0, .bss有时也会用.comm或.locomm

如:

static int i;

    .file    "test.c"

    .text

.lcomm i,4,4

.rodata:存放只读数据和变量,如字符串字面量
.data存放余下的数据和变量,可读可写

寄存器

分类:

通用寄存器(A/B/C/DX,BP,SP,DI,SP等)
状态和控制寄存器RFLAGS
指令寄存器RIP
XMM寄存器
浮点控制和状态寄存器MXCSR
等等

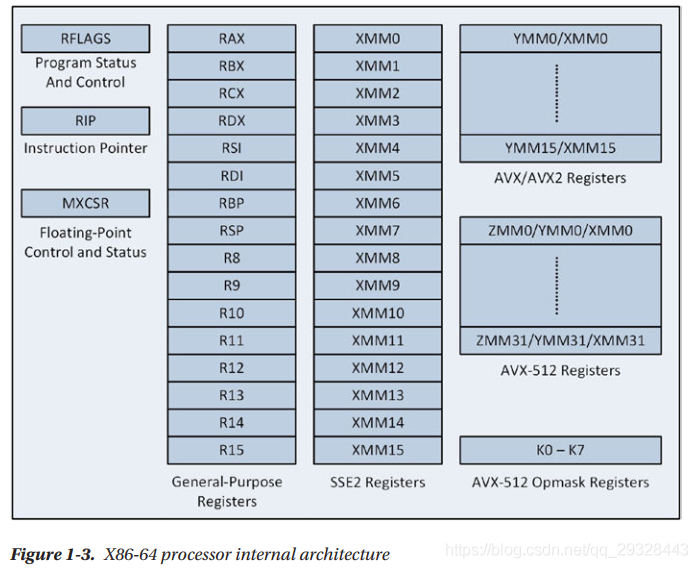
通用寄存器

主要用于算数,逻辑,比较运算,数据转移,地址计算,存放临时变量等

一个通用寄存器有4种用法,以RAX为例:

可以被当作RAX,64位
可以被当作EAX,32位
可以被当作AX,16位
可以被当作AL,8位

具体作用分类:

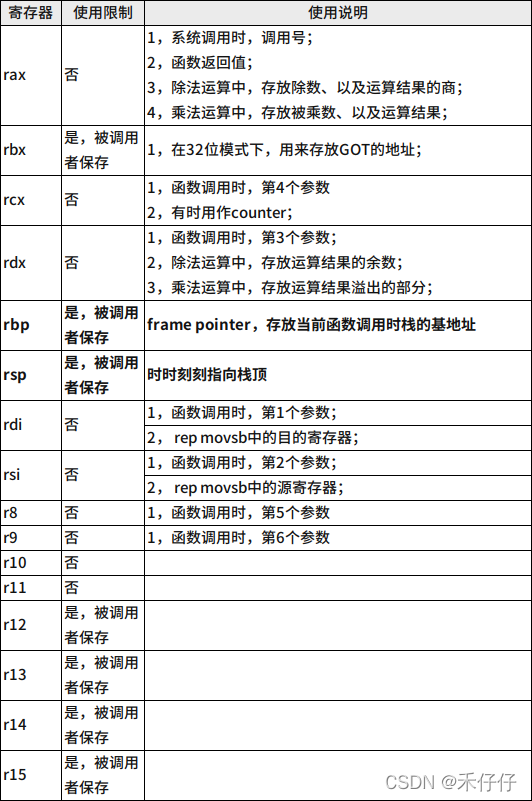
RFLAGS寄存器

RFLAGS和8086的FLAGS寄存器类似,也是用来存不同标记和状态的,但它是64位的,远比8086长,但常用的也就是那几个

常用的标记位:

进位标志位CF
溢出标志位OF
奇偶校验位PF
符号标志位SF
零标志位ZF

指令寄存器IP

指令寄存器RIP包含下一条将要被执行的指令的逻辑地址,通常情况下,每取出一条指令后,RIP会自动指向下一条指令,但遇到call和ret时,RIP会被修改

浮点数寄存器XMM/YMM/ZMM

XMM0-XMM15是一系列128位寄存器,用于

32位和64位浮点数的操作
SIMD指令:SIMD即Single Instruction Multiple Data,一条SIMD指令可以同时接受多个数据流

有效地址

$EffectiveAddress=BaseReg+IndexReg*ScaleFactor+Disp$

其中:

Basereg是基址寄存器,可以是任意一个通用寄存器
IndexReg是索引寄存器,可以是处理rsp之外的任一寄存器
ScaleFactor的取值可以是1,2,4,8
Disp是偏移量

最终得到的有效地址是64位的

各种寻址方式

Disp:访问全局变量或静态变量通常使用
BaseReg:常用于指针获取对应变量的值
BaseReg+Disp:常用于某种数据结构中的某个成员
IndexReg*SF+Disp:用于数组

指令集

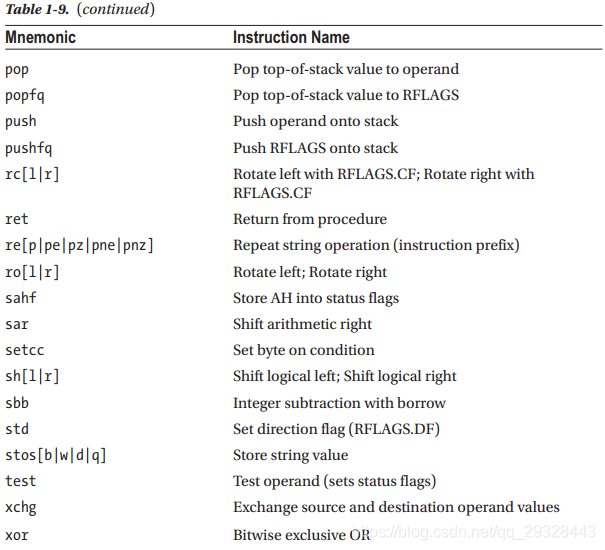
栈指令

push和pop

push R:

先将栈顶指令rsp减去8(8字节)
然后将R中目标操作数放入更新后的rsp所指向的地址处

pop R:

先将当前rsp所指的内容弹出到指定寄存器R
然后将rsp加8

call和ret

call f:

先将rip入栈,push %rip
再将函数f的第一条指令的地址赋给ip,mov f,%rip

ret:

弹出当前栈顶的地址到rip,pop %rip
继续执行