cs231n__3. LostFunction

CS231n

3.1 Lost Function

我们上次提到，要如何选择最优的W呢？

这就是要选择几种损失函数了。

我们要找到一种可行的方法来选择最优的W

先看简单的3个样本的例子

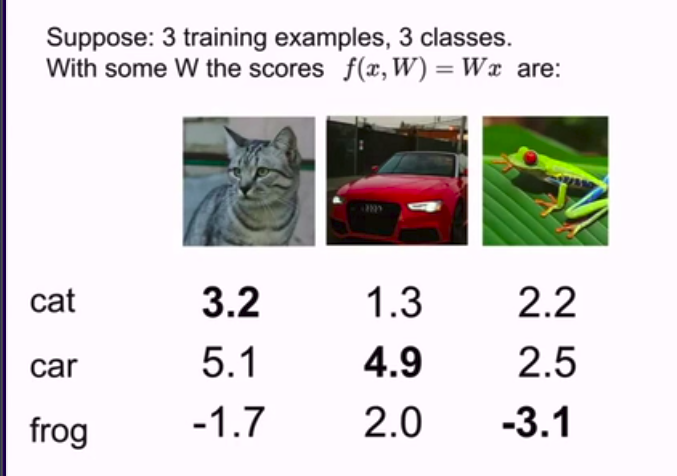
正式定义损失函数：

x是样本不带标签，y则是标签

在Cafar10，我们要把图片分类到10个类别中去。

所以，在这里，x代表图片，y则代表代表是个类别的数字，例如0到9的整数

这个公式其实在机器学习 中就见过超级多次了。

接下来我们来介绍细节：

我们先看对单个例子的损失函数：L_i

我们在所有错误的分类上做和，比较正确分类的分数和错误分类的分数。

如果正确分数比错误分数高出一个安全距离，则损失为0

otherwise 计算：

这个 1 ，是我们设定的边际。

BTW，这种某个值和 0 取 max的损失函数

也可以说成是一个合页损失函数

看图就明白了：

上图中x轴表示S_Yi ， 是训练样本真实分类的分数

y轴则是损失。

可以卡到随着真实分类的分数上升，则损失不断下降，这代表我们逐渐对样本分好了类。

（这里，S是通过分类器预测出来的类的分数）

（Y_i则是这个样本正确的分类标签）

• 1. 问题：这个式子到底在算什么？？*
     
     已知，如果真实分数中正确的分数比其他分数高出一段安全距离，我们会十分满意。反之，我们会得到一些 损失。那这些损失可以用这个式子来进行量化。

一个典型的例子（计算这个式子）

一言蔽之，这是在用一个量化衡量标准来计算偏差。

其他的样本也一样计算，然后把全部的L_i加起来求一个平均值。

• 1. 一个问题：为什么要加上一个 “ 1 ” ?*
     
     这其实是一个可以任意选择的值，相当于默认。
     
     你其实也可以加上其他的值，这个1其实并不重要。
• 1. 另一个问题：当你初始化这些参数并且从头开始训练，通常你先使用一些很小的随机值来初始化 W，你的分数的结果在训练的初期倾向于呈现较小的均匀值，并且问题在于如果你所有的S， 也就是你所有的分数都近乎为0并且差不多相等，那么当你使用多分类SVM的时候，损失函数预计会是如何呢？

  答：分类的数量减去 1 ！

  因为如果我们对所有不正确的类别遍历了一遍，那我们实际上遍历 了C-1个类别。在这些类别中的每一个这两个分数差不多相同，所以我们就会得到一个值为1的损失项，因为存在着1个边界，我们将会得到C-1。

  这是一个有用的debug策略！：
  
  当你开始训练的时候，你应该预想到你预期的损失函数该是多大，但如果在刚开始训练的时候你的损失函数，在第一次迭代的时候损失函数并不等于C-1.这意味着就可能有Bug

• 1. 另一个问题：全部求和会发生什么？（意思是求C个和而不是C-1个）
     
     答： 损失函数会加 1
     
     这个问题可以看成——去掉限制条件j≠yi时，总的loss值有什么变化？？？与之前求的loss比，多了当j=yi时的max（0，Sj-Syi+1）,这时Sj-Syi为0，求max得1，将这一项加到总的loss值，所以导致loss值加1.

• 1. 如果我们使用平均值而不是求和呢？
     
     不会改变！
     
     我们只是将损失函数缩放而已！

     衍生：如果我们改变公式怎么办？比如加一个平方？
     
     这样就会变！这意味着我们并不是计算同一个损失函数了。

代码：计算SVM损失函数

\(L_i = \sum_{j ≠ y_i}max(0,s_j - s_{y_i} + 1)\)

def L_i_vectorized(x, y, W):
    scores = W.dot(x)
# W.dot(x) 意思是W与x乘以点积
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

最后一个问题：当我们找到了一个完美的W，这个W是不是唯一？

答：不是！

如何选择W呢？我们可以画出曲线！

当然，这是一种机器学习的概念了，我们可以加上正则项。（这是机器学习的知识）

很多正则化知识和有关范数的知识。

正则化其实就是对参数的惩罚

主要目的是为了减轻模型的复杂度，而不是试图去拟合数据

当然我们要根据情况来判别用什么来拟合

这种情况下就是L2比较好

这点我们可以看西瓜书第11章

Softmax loss

multinomial logistic regression多项逻辑斯蒂回归

这个损失函数在深度学习中用的比较广泛

概率嘛。好像机器学习也学过啊。

所以真实的损失函数就要取log等等来返回来计算。

为增减性加了一个负号

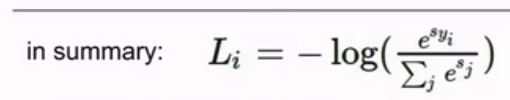
我们来看一个实例：

也叫多项式罗格斯回归

问题来了，softmax的最大值和最小值是什么？

0～Infinity

你永远无法得到0损失的结果

总结：

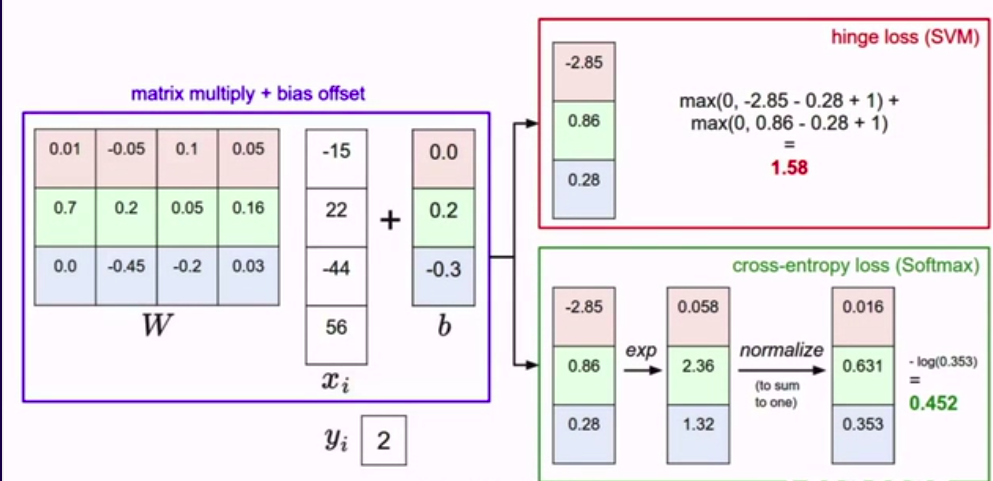
两个损失函数的区别

在线性中，变化一点点不会根本性改变结果

但在softmax的目标是将概率质量函数（离散分布值）等于 1 。所以，即使你给正确的样本再高的分，或者给错误的结果再低的分，softmax也会在这里积累更多的概率质量并不断往无穷大前进。

在SVM，它会正确识别后放弃，但softmax会试图让每一个数据点变得更好。

---

我们要记住一个debug方法：

在多类支持向量机的背景下，健全性检查问题

我们可以问softmax，如果所有的S都很小近乎为0 。损失值是多少？

ln（C）。如果不是则可能有bug

---

Recap

监督学习！

---

over!

3.2 Optimization

引例：

如何在这张图中找到山谷的底部？

1. 第一种坏方法：
   
   随机搜索

2. 利用几何形状
   
   例如，地面的倾斜
   
   最终到达谷底
   
   话说这不是梯度下降算法吗！！？？
   
   

   梯度就是偏导数的向量

梯度给出了函数在一阶上的逼近。

其中一个计算方法是：

有限差法：

基本上都是微积分的知识

就是加一小步逐渐逼近

直到收敛

当然我们不用这么复杂去计算这样一小步一小步。我们只要用到导数的知识

当然，也可以用数值梯度进行debug

就是使用数值梯度作为单元测试，来保证解析梯度是正确的。

下面就开始介绍深度学习的梯度下降算法

# Vanilla Gradient Descent

while True:
	weights_grad = evaluate_gradient(loss_fun, data, weights)
	weights += - step_size * weights_grad # perform parameter update

向梯度减小的方向上迈进一小步，不断重复

最后达到收敛。

但，步长是一个超参数.也叫学习率。是非常重要的一个超参数（一般要首要确定）

但是很多时候我们 的数据样本都是超级超级多的，所以这样的话每一次更新都要重头计算，这样非常麻烦，效率超级低，所以我们一般使用随机梯度下降，就和机器学习中的一模一样

每一次迭代都只选取一部分训练样本成为minibatch(小批量) 。 按惯例，都采用2的n次幂个，如32,64,128来估计。 然后，我们利用这一个minibatch来估算误差总和以及实际梯度。就是随机的，因为你可以把它当做对真实数值期望的一种蒙特卡洛估计。这就让我们的算法更高级。

---

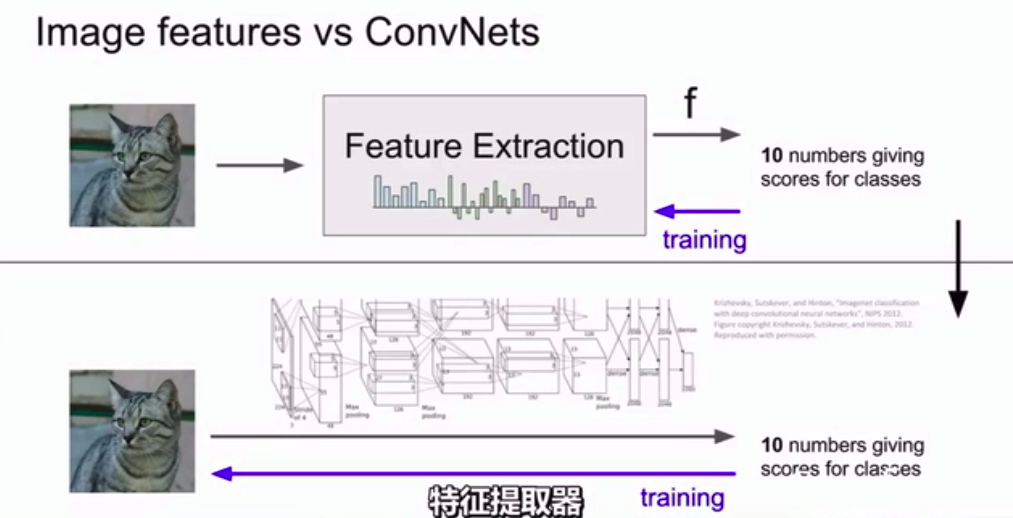
图像特征：

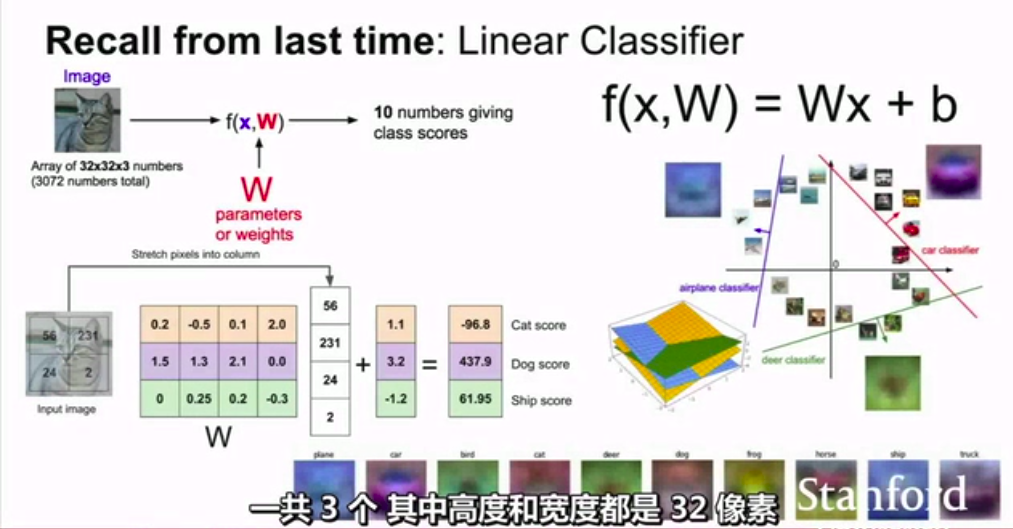
之前我们讲的线性分类器，是把图片的原始像素直接传入线性分类器。

但是这样做可能不太好，如多模态

所以当深度神经网络开始大规模运用之前，常用的方法就是实现两步走策略。

1. 拿到图片计算图片有关的特征值，如计算与图片形象有关的数值。然后把不同的特征向量合到一块得到图片的特征表述。
2. 然后，这一关于图片的特征表述（feature representation of image） 会作为输入源传入分类器。

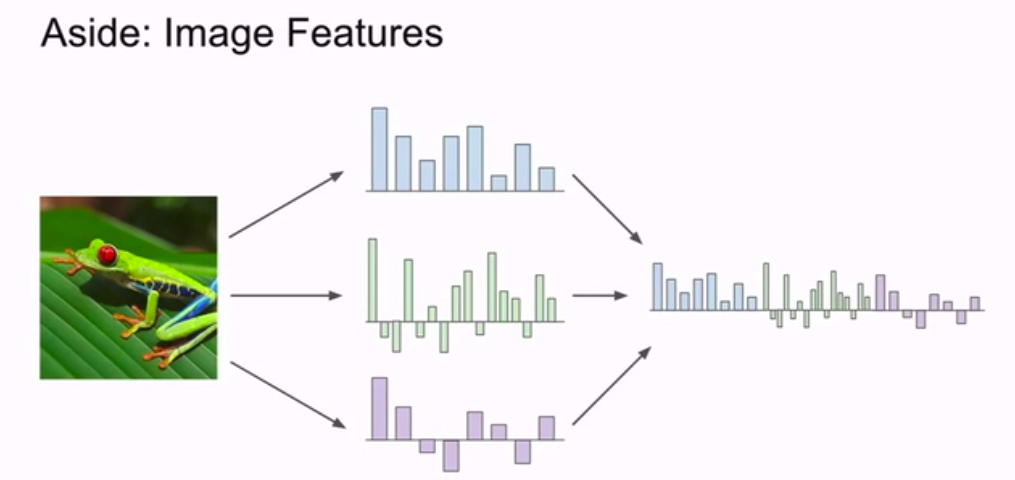
这样做的动机是什么？

通过实例来解释：

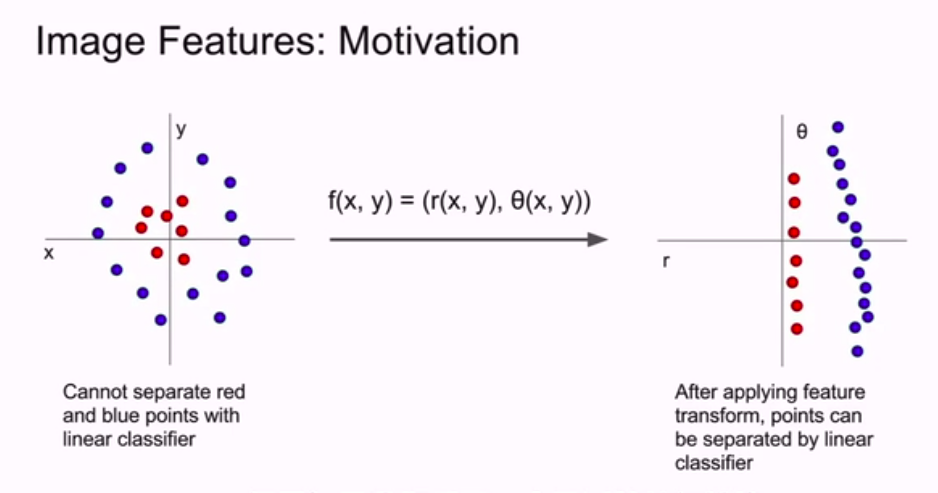
对于左边的这种，我们不可能用一条直线把红蓝分开，在这个例子中，我们利用极坐标转换，得到右边的图。

现在我们用特征转化就可以把复杂的数据集变成线性可分的，然后可以通过线性分类器正确分类。

这里我们的策略就是找出正确的特征转化。

一个非常简单的例子就是颜色直方图：

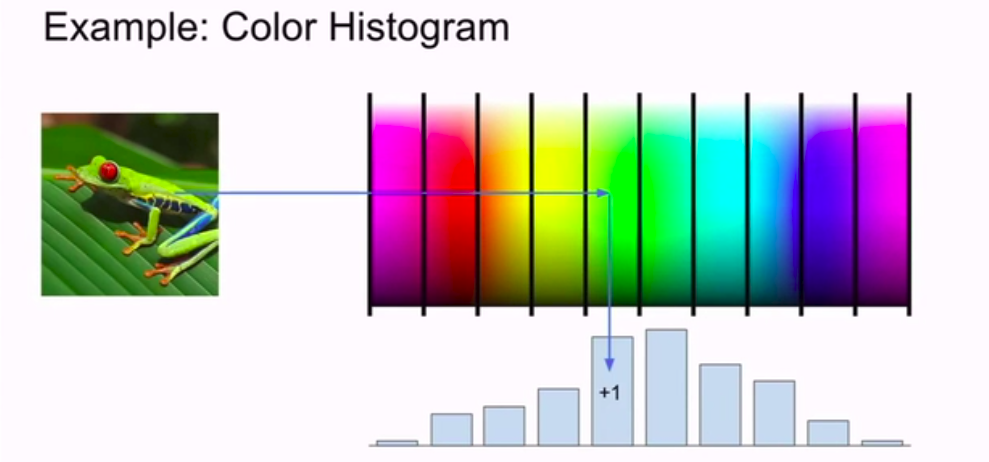
or

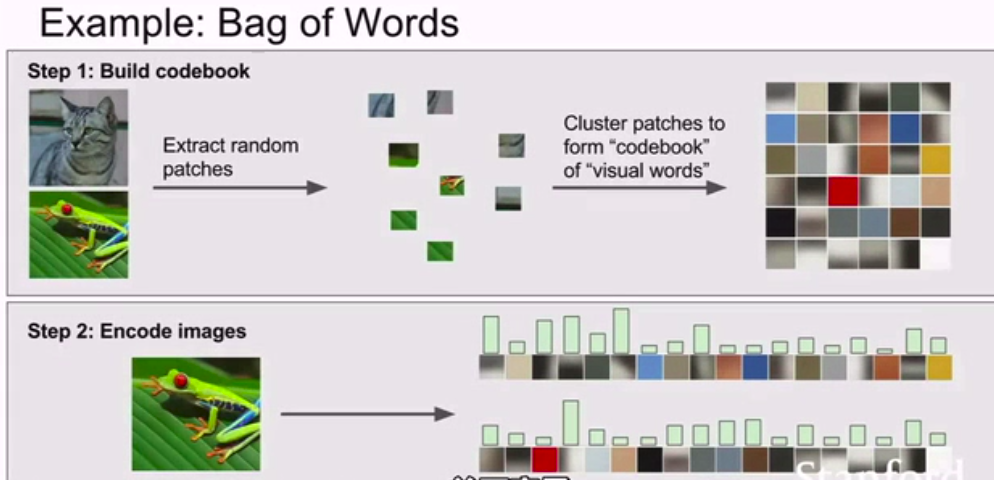
exclusion：