动态规划 洛谷P1616 疯狂的采药

动态规划 洛谷P1616 疯狂的采药

同样也是洛谷的动态规划一个普及－的题目，接下来分享一下我做题代码

看到题目，没很认真的看数据大小，我就提交了我的代码:

 1 //动态规划 洛谷P1616 疯狂的采药
 2 #include<iostream>
 3 #include<cmath>
 4 using namespace std;
 5 int value[10005];//价值数组
 6 int times[10005];//时间数组
 7 int dp[10000003];//t的范围1e7
 8 int main()
 9 {
10     int m, t;//m是数目，t是时间
11     cin >> t >> m;
12     for (int i = 1; i <= m; ++i)
13     {
14         cin >> times[i] >> value[i];//输入数据
15     }
16     //从小遍历到大进行规划 因为这题可以选无数个一样的
17     for (int i = 1; i <= t; ++i)
18     {
19         for (int j = 1; j <= m; ++j)//对每一种草药进行遍历
20         {
21             if (i >= times[j])//前提是时间大于采摘所需要的时间才能考虑
22             {
23                 dp[i] = max(dp[i], dp[i - times[j]] + value[j]);
24             }
25         }
26     }
27     cout << dp[t];
28     return 0;
29
30 }

测试了几个测试用例，过了 ，于是乎，我就自信满满的提交了！

但是！

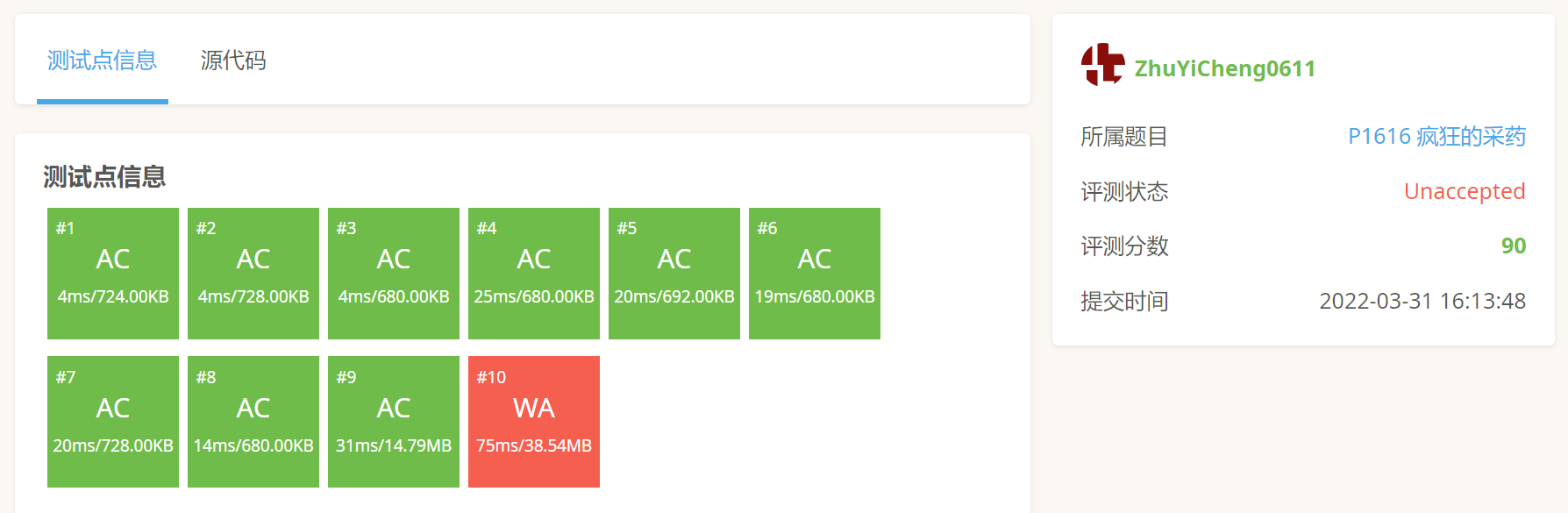
仔细观察数据大小，经典的没开long long

于是改正:

 1 //动态规划 洛谷P1616 疯狂的采药
 2 #include<iostream>
 3 #include<cmath>
 4 using namespace std;
 5 int value[10005];//价值数组
 6 int times[10005];//时间数组
 7 long long dp[10000003];//t的范围1e7 long long !!!!
 8 int main()
 9 {
10     int m, t;//m是数目，t是时间
11     cin >> t >> m;
12     for (int i = 1; i <= m; ++i)
13     {
14         cin >> times[i] >> value[i];//输入数据
15     }
16     //从小遍历到大进行规划 因为这题可以选无数个一样的
17     for (int i = 1; i <= t; ++i)
18     {
19         for (int j = 1; j <= m; ++j)//对每一种草药进行遍历
20         {
21             if (i >= times[j])//前提是时间大于采摘所需要的时间才能考虑
22             {
23                 dp[i] = max(dp[i], dp[i - times[j]] + value[j]);
24             }
25         }
26     }
27     cout << dp[t];
28     return 0;
29
30 }

然后！

结束啦！

总结归纳一下： 这题和P1048 [NOIP2005 普及组] 采药 非常像，只是数据加强了些，而且我们对比可以发现，还有一个区别就是每个药可以采摘无数次。

于是我们归纳出一个模板，像只能采摘一次，也就是选择一次的背包问题，我们用采摘时间time值来做外层循环，反正每次只能选择一次，也就是拿每种草药的时间来遍历.

//也就是
for(int i=1;i<=m;++i)
{
for(int j=x(背包的最大容量),j>=time[i],--j)
{
dp[j]=max(dp[j],dp[j-time[i]]+value[i]);
}
}

但是像这一题，每次可以选择无数次，我们外层循环就只能用时间了，有点像选硬币凑钱问题。从1一直遍历到最大的time。内层去遍历每一种草药，因为可以采摘多次，得出我们的模板：

for (int i = 1; i <= t（最大时间）; ++i)从小到大队每一个时间进行dp 算出每一个时间的最优解
    {
        for (int j = 1; j <= m（可供选择的种类数）; ++j)//对每一种草药进行遍历
        {
            if (i >= times[j])//前提是时间大于采摘所需要的时间才能考虑
            {
                dp[i] = max(dp[i], dp[i - times[j]] + value[j]);
            }
        }
    }