2019牛客多校A All-one Matrices——单调栈

题目

求非嵌套子矩阵的个数。

分析

单调栈的套路题（类似的有求最大子矩阵）。

首先，按列预处理，每个位置化成连续1的个数。

例如，左边的图转成右边。

                    

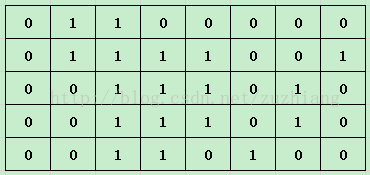
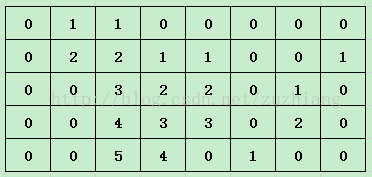
然后枚举每一行作为矩阵的底边，再从前往后枚举每一列，并维护一个关于高度的单调上升的栈。对于栈中每一个Up值，还需要维护一个其向左能拓展的最远位置Left（其实这个很容易实现，只需用一个普通的栈并与单调栈同步，同入同出）。

那么每当有元素退栈时，设退栈元素为 (Up, Left)，那么可以得到一个全1矩阵 (i-Up+1, Left) - (i, j)。

还需要判断这个矩阵能否会被更大的矩形嵌套，随便用一种方法判断一下。例如，用 C[left] [right] 表示以 left-right 为宽的矩形延伸到了哪一行。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn =  + ;
int n, m, A[maxn][maxn], B[maxn][maxn], C[maxn][maxn];
char s[maxn];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = ;i < n;i++)
    {
        scanf("%s", s);
        for(int j = ;j < m;j++)  A[i+][j+] = s[j] - '';
    }
    for(int j = ;j <= m;j++)
        for(int i = ;i <= n;i++)
        {
            if(A[i][j] == )  B[i][j] = B[i-][j] + ;
            else B[i][j] = ;
        }

    ll ans = ;
    memset(C, -, sizeof(C));
    for(int i = ;i <= n;i++)
    {
        stack<int>st1, st2;
        for(int j = ;j <= m+;j++)
        {
            int left = j;
            while(!st1.empty() && B[i][j] < st1.top())
            {
                if(C[st2.top()][j] != i - )  ans++;    //与上一层不是同一个最大矩形时
                C[st2.top()][j] = i;
                st1.pop();
                left = st2.top();
                st2.pop();
            }

            if((st1.empty() && B[i][j] != ) || (!st1.empty() && B[i][j] > st1.top()))
            {
                st1.push(B[i][j]);
                st2.push(left);
            }
        }
    }
    printf("%lld\n", ans);
    return ;
}

参考链接： https://blog.csdn.net/zuzhiang/article/details/78693421