拓扑排序的 +Leapms 线性规划模型

知识点

拓扑排序

拓扑排序的+Leapms模型

无圈有向图

一个图G(V,E), 如果边有向且不存在回路，则为无圈有向图。在无圈有向图上可以定义拓扑排序。下图是一个无圈有向图的例子。

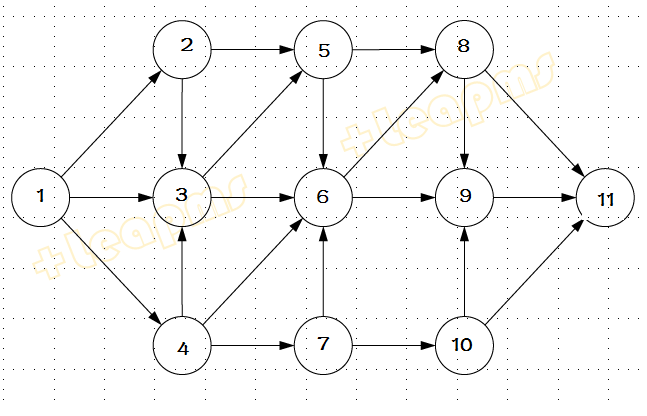
拓扑排序

给定一个无圈有向图G(V,E)，对其顶点集合V中的元素进行排序，使得对任何两个顶点v1,v2，如果(v1,v2)是图上的一条边，则在排序中v1优先于v2.

拓扑排序的+Leapms模型

对图G(V,E)中的边的表示可以用其起始边和终止边表示，对第k条边，其起始定点使用函数alpha[k]表示，其终止顶点用beta[k]表示。

设m是图中的边数，n是图中的顶点数。设x[i]是顶点i的次序数（拓扑排序中允许并列次序，例如并列第2等等）。

于是对任意一条边，其终止顶点的次序数一定至少比其起始顶点的次序数大至少1。于是有约束：

x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m

希望至少从1开始编号次序数，于是有另外的约束：

x[i]>=1|i=1,...,n

为了对次序数进行紧凑编号，模型的目标设为极小化所有次序数的和：

min sum{i=1,...,n}x[i]

完整的+Leapms模型为：

min sum{i=1,...,n}x[i]
subject to
	x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m
	x[i]>=1|i=1,...,n

where
	m,n are integers
	e is a set
	alpha[k],bata[k] are integers| k=1,...,m
	x[i] is a variable of nonnegative number| i=1,...,n

data_relation
	m=_$(e)/2
	alpha[k]=e[2k-1]  | k=1,...,m
	bata[k]=e[2k] | k=1,...,m
	n=0
	n=max(n,alpha[k]) | k=1,...,m
	n=max(n,bata[k]) | k=1,...,m

data
    e={
	(1 2)
	(1 3)
	(1 4)
	(2 3)
	(2 5)
	(3 5)
	(3 6)
	(4 6)
	(4 7)
	(5 6)
	(5 8)
	(6 8)
	(6 9)
	(7 6)
	(7 10)
	(8 9)
	(8 11)
	(9 11)
	(10 9)
	(10 11)
    }

求解过程

+Leapms>load
 Current directory is "ROOT".
 .........
        toposort.leap
 .........
please input the filename:toposort
================================================================
1:  // x[i] 是 i点的拓扑排序层次
2:
3:  min sum{i=1,...,n}x[i]
4:  subject to
5:      x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m
6:      x[i]>=1|i=1,...,n
7:
8:  where
9:      m,n are integers
10:     e is a set
11:     alpha[k],bata[k] are integers| k=1,...,m
12:     x[i] is a variable of nonnegative number| i=1,...,n
13:
14:  data_relation
15:     m=_$(e)/2
16:     alpha[k]=e[2k-1]  | k=1,...,m
17:     bata[k]=e[2k] | k=1,...,m
18:     n=0
19:     n=max(n,alpha[k]) | k=1,...,m
20:     n=max(n,bata[k]) | k=1,...,m
21:
22:  data
23:      e={
24:     (1 2)
25:     (1 3)
26:     1 4
27:     2 3
28:     2 5
29:     3 5
30:     3 6
31:     4 6
32:     4 7
33:     5 6
34:     5 8
35:     6 8
36:     6 9
37:     7 6
38:     7 10
39:     8 9
40:     8 11
41:     9 11
42:     10 9
43:     10 11
44:      }
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=11
number of constraints=31
..................................
+Leapms>mip
relexed_solution=45; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
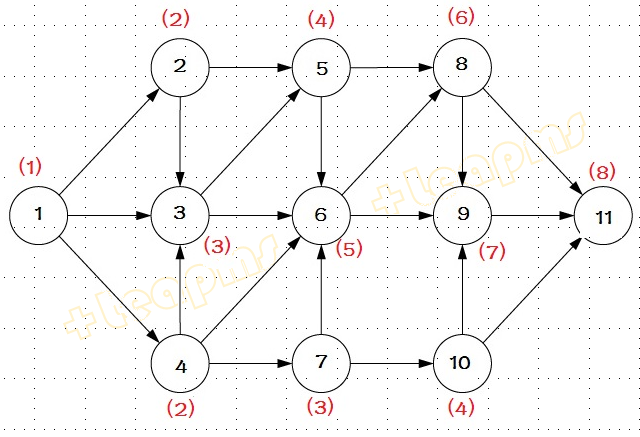
找到整数规划的最优解.非零变量值和最优目标值如下：
  .........
    x1* =1
    x2* =2
    x3* =3
    x4* =2
    x5* =4
    x6* =5
    x7* =3
    x8* =6
    x9* =7
    x10* =4
    x11* =8
  .........
    Objective*=45
  .........
+Leapms>

标记在图上

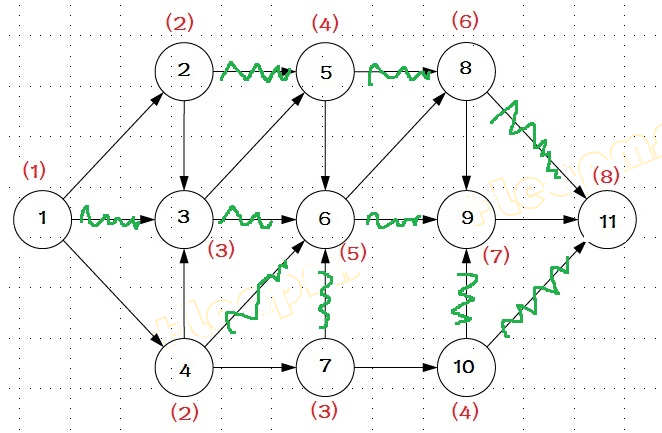
拓扑排序的用途

拓扑排序在算法设计上有广泛的用途，例如在制造资源管理中的Gozinto图的计算等。

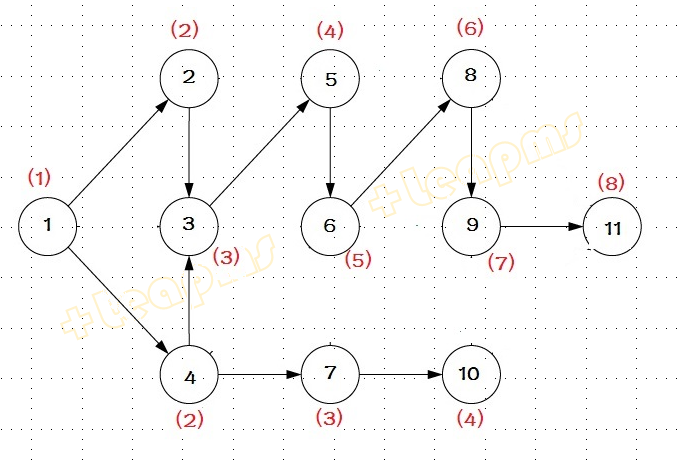
对上述图如果有向边表示次序关系，则可删除任何起始顶点和终止顶点次序数相差大于2的边得到更加简化的图，且不改变次序逻辑：