指针-AC自动机

大家都不喜欢指针，但是这个AC自动机仿佛不用不行……

先引用我最喜欢的话：“AC自动机，不是自动AC的机器。” 如果写不好还可能一直WA

AC自动机是KMP与Trie树的完美结合，适用于多字符串匹配，这与KMP的单串不同

首先是一棵Trie树

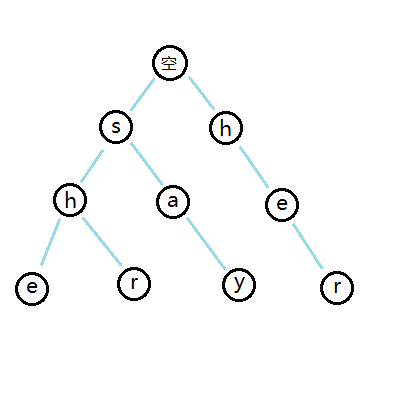
记得建空节点做根，有大神忘记了建，直想砸键盘。

然后标准建树

如果用指针的话申请空间冷静一点

下一步就是构建fail指针，虽然我喜欢把它叫next，与KMP一致

幸好找到了好的版子，不然就很难搞

因为fail指针的构建顺序必须由上到下

即：fail是从下面的节点指向上面的节点的，这样不会漏配

So用BFS会很棒。

左面就是一个手画的树

---

void build(){
    root->next=NULL;//根节点无fail
    push(root);//根节点入队
    while(!empty()){//BFS开始
        TREE *i=front();//提取队首元素
        for(int j=;j<;j++){//对每一个字母进行处理，尝试搜索
            if(i->s[j]!=NULL){//搜到
                if(i==root)i->s[j]->next=root;//是和根节点直接连的回根
                else
                {
                    TREE* p=i->next;//和搜索的点的fail指针的下节点找
                    while(p!=NULL)//继续找，所有fail都符合要求
                    {
                        if(p->s[j]!=NULL)//fail指针处有和j字母一样的点
                        {
                            i->s[j]->next=p->s[j];//更新结束
                            break;
                        }
                        p=p->next;//fail的fail也符合要求
                    }
                    if(p==NULL) i->s[j]->next=root;//无匹配，回根
                }
                q[++e]=i->s[j];//结果入队
            }
        }
    }
}

经过一番建立，我们将所有的fail构建完成~~

长这样:

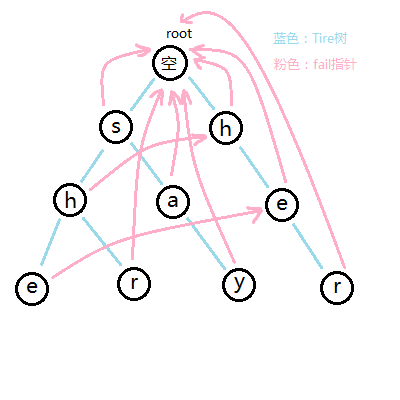最好自己再画一个图，这样会更好的理解

然后就要搜索了，搜索和建立很像

补下：搜索的解释，上次忘写了，自己很吃亏，尴尬

void ffind(){//搜索函数
    int j=;//从0号位开始搜
    TREE *p=root;//另一方面树上从根节点走起
    while(st[j])
    {
        int i=st[j]-'a';//不解释
        while(p->s[i]==NULL && p!=root) p=p->next;//没找着，就顺着fail往下走
        p=p->s[i];//这时只可能有两种可能，一是真没有，二是找着一个
        if(p==NULL)p=root;//没有我们直接回根，相当于重置树上指针
        TREE *k=p;//这个是找着后用的
        while(k!=root && k->endt!=-)//去找
        {
            ans+=k->endt;//有结尾标记，这个是根据KeywordSearch的题意
            k->endt=-;//为了防止重复计算 ，这个也是题意
            k=k->next;//到所有的fail指针处找
        }
        j++;
    }
}

如果是搜是否匹配或出现次数，在结尾写cnt计数即可

但如果要算匹配长度，我们就要打标记，再dfs一遍，像玄武密码一样

下面补上题和码

[模板]Keyword Search

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <queue>
 #define  L 1010101
 using namespace std;
 struct TREE{
     TREE *next,*s[];
     char dat;
     int endt;
     TREE(){
         next=NULL;
         memset(s,,sizeof s);
         dat=endt=;
     }
 };
 TREE *q[];
 int f=,e=;
 TREE *root;
 int n,ans=;
 char ch[L],st[L];
 void add(char *now){
     TREE *i=root;
     int j=;
     while(now[j]){
         int k=now[j]-'a';
         if(i->s[k]==NULL)
             i->s[k]=new TREE();
         i=i->s[k];
         j++;//cout<<j<<endl;getchar();puts("P");
     }
     i->endt++;
 }
 bool empty(){
     if(e==f){
         return true;
     }
     return false;
 }
 void push(TREE *i){
     e++;
     q[e]=i;
 }
 TREE* front(){
     if(empty())return NULL;
     f++;
     return q[f];
 }
 void build(){
     root->next=NULL;
     push(root);
     while(!empty()){
         TREE *i=front();
         for(int j=;j<;j++){
             if(i->s[j]!=NULL){
                 if(i==root) i->s[j]->next=root;
                 else
                 {
                     TREE* p=i->next;
                     while(p!=NULL)
                     {
                         if(p->s[j]!=NULL)
                         {
                             i->s[j]->next=p->s[j];
                             break;
                         }
                         p=p->next;
                     }
                     if(p==NULL) i->s[j]->next=root;
                 }
                 q[++e]=i->s[j];
             }
         }
     }
 }
 void ffind(){
     int j=;
     TREE *p=root;
     while(st[j])
     {
         int i=st[j]-'a';
         while(p->s[i]==NULL && p!=root) p=p->next;
         p=p->s[i];
         if(p==NULL)p=root;
         TREE *k=p;
         while(k!=root && k->endt!=-)
         {
             ans+=k->endt;
             k->endt=-;
             k=k->next;
         }
         j++;
     }
 }
 int main(){
     int T;
     scanf("%d",&T);
     while(T--){
         root=new TREE();
         ans=;
         scanf("%d",&n);
         for(int i=;i<=n;i++){
             scanf("%s",ch);
             add(ch);
         }
         scanf("%s",st);
         build();
         ffind();
         printf("%d\n",ans);
     }
     return ;
 }

[稍有思考][还是模板]玄武密码

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #define L 111111111
 #define N 111111
 using namespace std;
 struct ACauto{
     ACauto *next,*s[];
     int endp,DeepinC;
     bool mark;
     ACauto(){
         next=NULL;
         memset(s,,sizeof s);
         mark=DeepinC=endp=;
     }
 }*root;
 struct Myqueue{
     ACauto *Q[];int f,e;
     bool empty(){
         if(e==f)return true;
         return false;
     }
     void push(ACauto *k){
         e++;
         Q[e]=k;
     }
     ACauto* front(){
         if(empty())return NULL;
         f++;
         return Q[f];
     }
 }q;
 int n,ans=,cnt=;
 char st[L],ch[N][];
 inline int turn(char ch){
     switch(ch){
         case 'E':return ;
         case 'W':return ;
         case 'S':return ;
         default :return ;
     }
 }
 void add(char *c){
     ACauto *i=root;
     int j=;
     while(c[j]){
         int k=turn(c[j]);
         if(i->s[k]==NULL)
             i->s[k]=new ACauto();
         i=i->s[k];
         i->DeepinC=j+;
 //        cout<<c[j]<<" "<<i->DeepinC<<endl;
         j++;
     }
     i->endp++;
 }
 void build(){
     root->next=NULL;
     q.push(root);
     while(!q.empty()){
         ACauto *i=q.front();
         for(int j=;j<;j++){
             if(i->s[j]!=NULL){
                 if(i==root) i->s[j]->next=root;
                 else{
                     ACauto *p=i->next;
                     while(p!=NULL){
                         if(p->s[j]!=NULL){
                             i->s[j]->next=p->s[j];
                             break;
                         }
                         p=p->next;
                     }
                     if(p==NULL) i->s[j]->next=root;
                 }
                 q.push(i->s[j]);
             }
         }
     }
 }
 void ffind(char *ser){
     int j=;
     ACauto *p=root;
     while(ser[j]){
         int i=turn(ser[j]);
         while(p->s[i]==NULL&&p!=root){
             p=p->next;
             p->mark=;//cout<<p<<" INP  "<<j<<" "<<ser[j]<<" Depth: "<<p->mark<<" "<<p->DeepinC<<endl;
         }
         p=p->s[i];
         if(p==NULL)p=root;
         ACauto *k=p;
         while(k!=root && k->endp!=-){
             k->mark=;
             k->endp=-;
             k=k->next;//cout<<k<<" INK  "<<j<<" "<<ser[j]<<" Depth: "<<k->mark<<" "<<k->DeepinC<<endl;
         }
 //        cout<<k<<" OUTK "<<j<<" "<<ser[j]<<" Depth: "<<k->mark<<" "<<k->DeepinC<<endl;
         j++;
     }
 }
 void ser(char *c){
     ACauto *i=root;
     int j=;
     int lsans=;
     bool la=;
     while(c[j]){
         int k=turn(c[j]);
         i=i->s[k];
         if(i->mark)ans=max(i->DeepinC,ans);
         j++;
     }
 }
 int main(){
     int len;
     root=new ACauto();
     scanf("%d%d",&len,&n);
     scanf("%s",st);
     for(int i=;i<=n;i++) {
         scanf("%s",ch[i]);
         add(ch[i]);
     }
     build();
     ffind(st);
     for(int i=;i<=n;i++){
         ans=;
         ser(ch[i]);
         printf("%d\n",ans);
     }
     return ;
 }