【loj6034】「雅礼集训 2017 Day2」线段游戏

#6034. 「雅礼集训 2017 Day2」线段游戏

内存限制：256 MiB　时间限制：1000 ms　标准输入输出

题目类型：传统　评测方式：Special Judge

上传者： 匿名

题目描述

给出若干条线段，用 (x1,y2),(x2,y2) 表示其两端点坐标，现在要求支持两种操作：

• 0 x1 y1 x2 y2 表示加入一条新的线段 (x1,y2),(x2,y2)；
• 1 x0 询问所有线段中，x 坐标在 x0 处的最高点的 y 坐标是什么，如果对应位置没有线段，则输出 0 。

输入格式

第一行两个正整数 n 、m 为初始的线段个数和操作个数。
接下来 n 行，每行四个整数，表示一条线段。
接下来 m 行，每行为一个操作 0 x1 y1 x2 y2 或 1 x0。

输出格式

对于每一个询问操作，输出一行，为一个实数，当你的答案与标准答案误差不超过10^-2时，则视为正确。

样例

样例输入

3 4
0 -1 4 1
4 2 7 2
7 1 8 2
1 4
1 3
0 3 3 6 3
1 3

样例输出

2
0.5
3

数据范围与提示

对于 10% 的数据，n,m≤1000；
对于另外 20% 的数据，所有的 1 操作都在 0 操作之后；
对于另外 20% 的数据，所有线段的两端的 x 坐标都包含所有询问的 x 坐标，你可以将每条线段当做直线处理；
对于 100% 的数据，1≤n≤50000,1≤m≤150000 ，x1,x2,y1,y2 均为整数，0<x0≤10^5,−10^6≤x1,x2,y1,y2≤10^6。

题意：

在平面直角坐标系中给你$n$条线段，$m$次询问，每次询问$x$处一条$y$值最大的线段。

题解：

容易发现我们需要用一个数据结构维护每个$x$处$y$最大的线段，支持查询，修改操作。

考虑线段树维护覆盖$[l,r]$区间的$y$最大线段是否可行。

但如果两条线段同时覆盖$[l,r]$且交点在$[l,r]$内则无法确定取哪条。

换句话说，一条线段如果没有被完爆就都是有贡献的。

但如果我们考虑维护覆盖$[l,r]$区间且在$mid$处$y$最大的线段呢？

（子区间不维护与父区间相同的线段）

反证法易得，过$x$处最大的线段必然在线段树上从$[1,N]$到$[x,x]$的路径上任意一处$mid$最大。

这是一棵不下传父节点标记的标记永久化线段树，专业名词叫做李超树。

现在维护应该十分好想了。

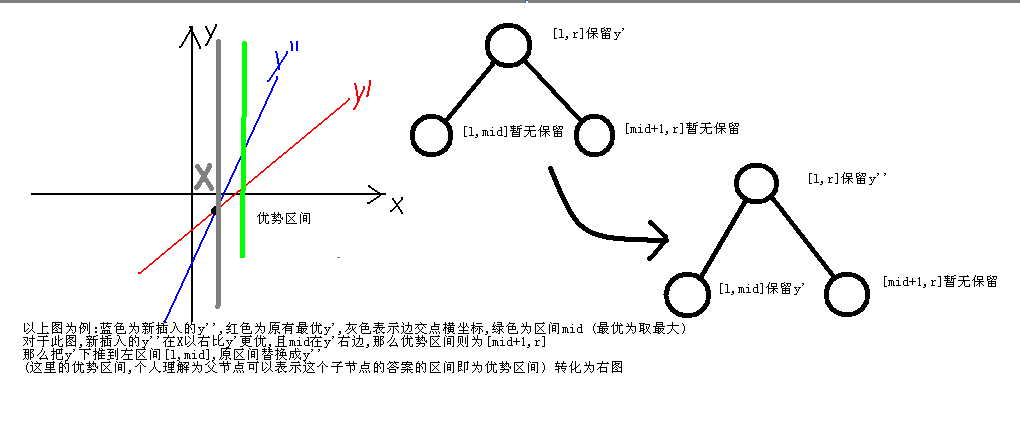
（转自网络dalao，侵删）

每当在区间$[l,r]$更新一条线段时，

• 若该线段没有完全覆盖该区间，则更新左儿子，右儿子
• 若该线段完爆了该区间原有的线段，直接替换并不更新儿子
• 若该线段在$mid$处大于该区间原有线段，将该区间维护的线段更新为该线段　　
  • 若该线段斜率大于原有线段，则原有线段在$[l,mid]$处可能有贡献，在$[mid+1,r]$处不可能有贡献，用原有线段更新左儿子
  • 若该线段斜率小于原有线段，则原有线段在$[l,mid]$处不可能有贡献，在$[mid+1,r]$处可能有贡献，用原有线段更新右儿子
• 若该线段在$mid$处小于该区间原有线段
  • 若该线段斜率大于原有线段，则该线段在$[l,mid]$处不可能有贡献，在$[mid+1,r]$处可能有贡献，用该线段更新右儿子
  • 若该线段斜率小于原有线段，则该线段在$[l,mid]$处可能有贡献，在$[mid+1,r]$处不可能有贡献，用该线段更新左儿子

查询时在线段树访问叶节点$[x0,x0]$的路径上取$max$即可。

线段维护双点或点截距均可。

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;
#define MAXN 100005
#define MAXM 500005
#define INF 0x7fffffff
#define ll long long

struct node{
    int l,r,x1,x2;
    double y1,y2;
    node(){
        x1=-1e6;x2=1e6;
        y1=y2=-1e7;
    }
}tree[MAXN<<];
inline int read(){
    int x=,f=;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-;
    for(;isdigit(c);c=getchar())
        x=x*+c-'';
    return x*f;
}

double gety(int x0,int x1,int x2,double y1,double y2){
    if(x1==x2) return max(y1,y2);
    double k=(y1-y2+0.0)/(x1-x2+0.0);
    double b=(y1+0.0)-k*(x1+0.0);
    return k*(x0+0.0)+b;
}

void build(int l,int r,int k){
    //cout<<l<<":"<<r<<":"<<k<<endl;
    tree[k].l=l,tree[k].r=r;
    if(l==r) return;
    int mid=(l+r)>>;
    build(l,mid,k<<);
    build(mid+,r,k<<|);
    return;
}

void insert(int x1,int x2,double y1,double y2,int k){
    int mid=(tree[k].l+tree[k].r)>>;
    //cout<<k<<":"<<tree[k].l<<":"<<tree[k].r<<endl;
    if(tree[k].l>x2 || tree[k].r<x1) return;
    if(x1<=tree[k].l && tree[k].r<=x2){
        if(gety(mid,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)<gety(mid,x1,x2,y1,y2)){
            //cout<<mid<<" "<<x1<<" "<<x2<<" "<<y1<<" "<<y2<<endl;
            if(gety(tree[k].l,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)>gety(tree[k].l,x1,x2,y1,y2)) insert(tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2,k<<);
            if(gety(tree[k].r,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)>gety(tree[k].r,x1,x2,y1,y2)) insert(tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2,k<<|);
            tree[k].x1=x1,tree[k].x2=x2;tree[k].y1=y1,tree[k].y2=y2;
        }
        if(gety(mid,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)>gety(mid,x1,x2,y1,y2)){
            if(gety(tree[k].l,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)<gety(tree[k].l,x1,x2,y1,y2)) insert(x1,x2,y1,y2,k<<);
            if(gety(tree[k].r,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2)<gety(tree[k].r,x1,x2,y1,y2)) insert(x1,x2,y1,y2,k<<|);
        }
        return;
    }
    if(x1<=mid) insert(x1,x2,y1,y2,k<<);
    if(x2>mid) insert(x1,x2,y1,y2,k<<|);
    return;
}

double query(int x0,int k){
    if(tree[k].l==tree[k].r)
        //cout<<k<<":"<<tree[k].l<<":"<<tree[k].r<<endl;
        return gety(x0,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2);
    int mid=(tree[k].l+tree[k].r)>>;
    double t1=gety(x0,tree[k].x1,tree[k].x2,tree[k].y1,tree[k].y2);
    //cout<<x0<<":"<<tree[k].x1<<":"<<tree[k].x2<<":"<<tree[k].y1<<":"<<tree[k].y2<<endl;
    //cout<<t1<<endl;
    if(x0<=mid) return max(t1,query(x0,k<<));
    else return max(t1,query(x0,k<<|));
}

int main(){
    //freopen("C1.in","r",stdin);
    //freopen("segment.out","w",stdout);
    int N=read(),M=read();
    build(,1e5,);
    for(int i=;i<=N;i++){
        int x1,x2;
        double y1,y2;
        cin>>x1>>y1>>x2>>y2;
        if(x1>x2) swap(x1,x2),swap(y1,y2);
        insert(x1,x2,y1,y2,);
    }
    for(int i=;i<=M;i++){
        int flag=read();
        if(!flag){
            int x1,x2;
            double y1,y2;
            cin>>x1>>y1>>x2>>y2;
            if(x1>x2) swap(x1,x2),swap(y1,y2);
            insert(x1,x2,y1,y2,);
        }
        else{
            int x0;cin>>x0;
            double k=query(x0,);
            if(k==-1e7) printf("%d\n",);
            else printf("%.2lf\n",k);
        }
    }
    return ;
}
/*
3 4
0 -1 4 1
4 2 7 2
7 1 8 2
1 4
1 3
0 3 3 6 3
1 3
*/