S - Cyclic Components （并查集的理解）

Description

You are given an undirected graph consisting of n vertices and m edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex a is connected with a vertex b, a vertex b is also connected with a vertex a). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices u and v belong to the same connected component if and only if there is at least one path along edges connecting u and v.

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

the first vertex is connected with the second vertex by an edge,
the second vertex is connected with the third vertex by an edge,
...
the last vertex is connected with the first vertex by an edge,
all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

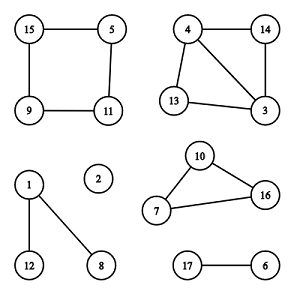
There are 6 connected components, 2 of them are cycles: [7,10,16] and [5,11,9,15].

Input

The first line contains two integer numbers n and m (1≤n≤$2⋅10^5$, 0≤m≤$2⋅10^5$) — number of vertices and edges.
The following m lines contains edges: edge i is given as a pair of vertices vi, ui (1≤vi,ui≤n, ui≠vi). There is no multiple edges in the given graph, i.e. for each pair (vi,ui) there no other pairs (vi,ui) and (ui,vi) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Input

Output

Input

Output

Note

In the first example only component [3,4,5] is also a cycle.

The illustration above corresponds to the second example.

解题思路：并查集的运用。判断单环的条件为判断每个集合（连通分量，同一个祖先节点）中所有点的度数是否都为2，并且该集合中元素的个数至少为3个，满足这两个条件才可构成单环。

AC代码：

 #include<bits/stdc++.h>

 using namespace std;

 const int maxn=;

 int n,m,a,b,c,cnt,fa[maxn],Deg[maxn];vector<int> vec[maxn];

 void init(){//初始化

     for(int i=;i<=n;++i)fa[i]=i;

 }

 int findt(int x){

     int per=x,tmp;

     while(fa[per]!=per)per=fa[per];

     while(x!=per){tmp=fa[x];fa[x]=per;x=tmp;}//路径压缩

     return x;

 }

 void unite(int x,int y){

     x=findt(x),y=findt(y);

     if(x!=y)fa[x]=y;

 }

 int main(){

     cin>>n>>m;

     init();cnt=;

     memset(Deg,,sizeof(Deg));

     for(int i=;i<=n;++i)vec[i].clear();//清空

     while(m--){

         cin>>a>>b;

         unite(a,b);

         Deg[a]++;Deg[b]++;//每个顶点的度数加1

     }

     for(int i=;i<=n;++i)//把同一个祖先所有的节点放在一个邻接表中

         vec[findt(i)].push_back(i);

     for(int i=;i<=n;++i){

         if(vec[i].size()>){//构成单环的点的个数至少为3个

             bool flag=false;

             for(size_t j=;j<vec[i].size();++j)

                 if(Deg[vec[i][j]]!=){flag=true;break;}//如果度数不为2的，直接退出

             if(!flag)cnt++;//如果是单环，计数器就加1

         }

     }

     cout<<cnt<<endl;

     return ;

 }