2024Jiangxi_H Convolution

Description

Input

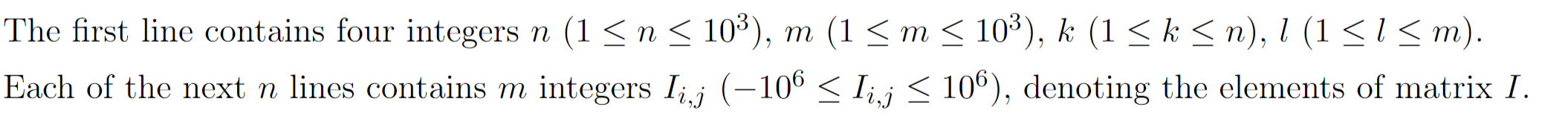
Output

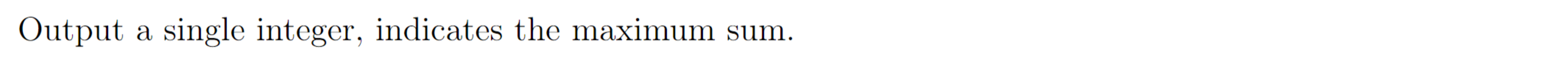
Sample Input

5 5 3 3
0 -1 -1 0 0
0 1 -1 2 -2
2 -2 2 2 0
-1 0 0 -2 -1
0 -2 0 1 1

Sample Output

12

Explainion

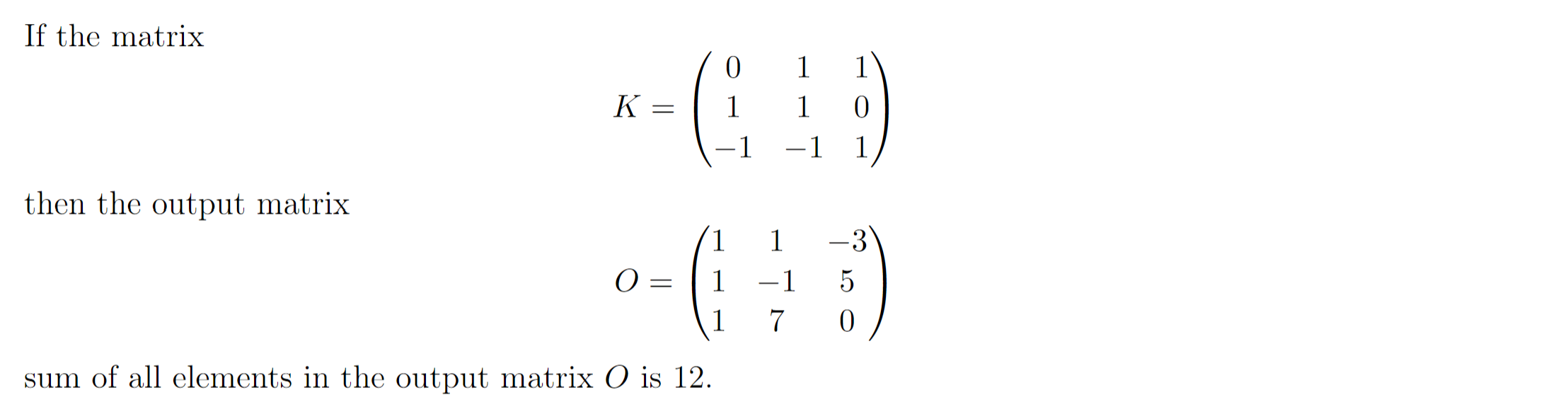
Hint

• 卷积运算规则
• 二维前缀和

Thinking

• 这道题的题目背景是卷积运算规则。我们首先得了解卷积运算方式。我们不难发现\(K_{i,j}\) 产生的贡献是\(K_{i,j}\) × 矩阵 \(I_{i,j ~ n−k+i,m−l+j}\)的子矩阵之和。
  
  
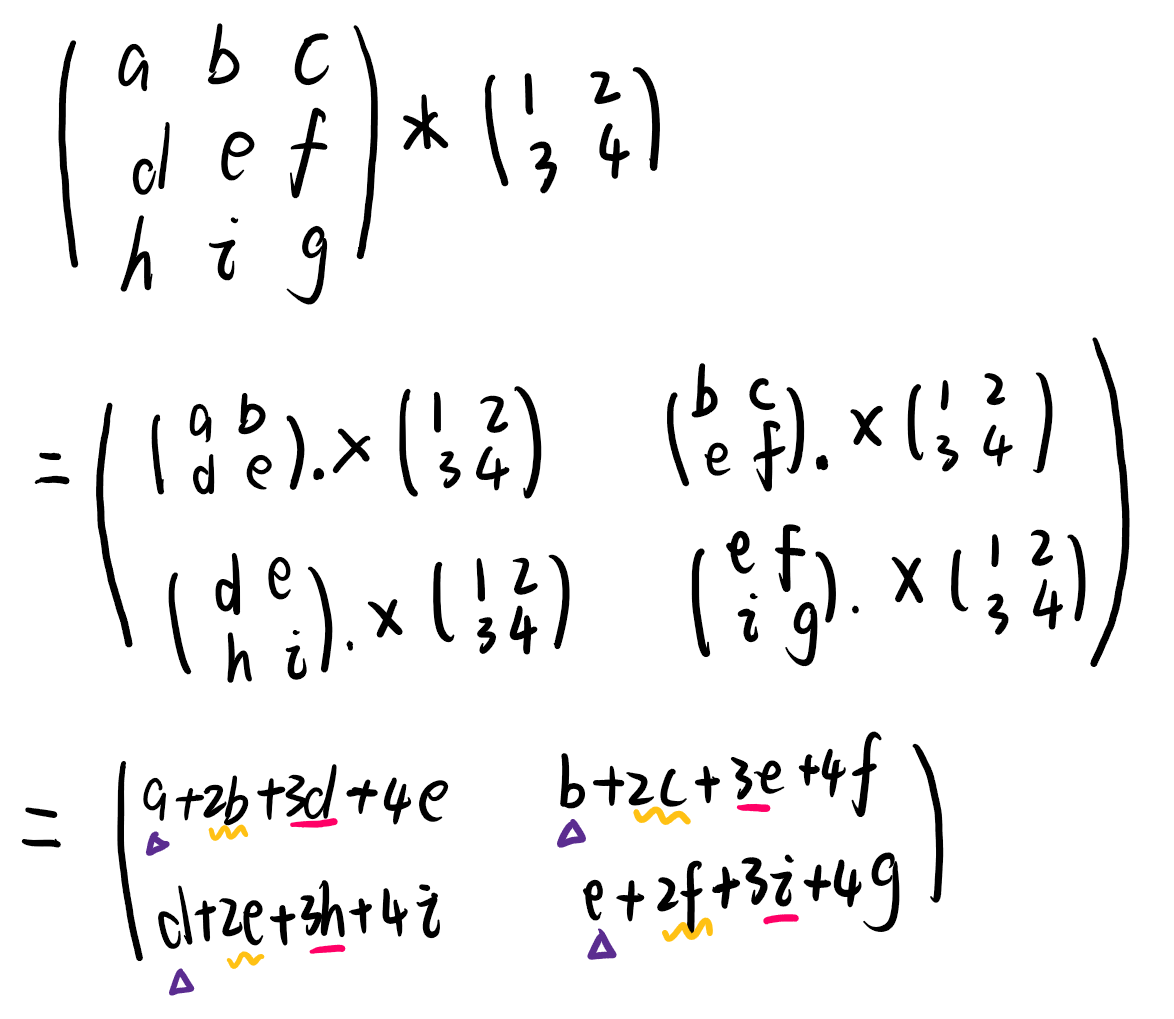
• 于是我们就可以据此确定K矩阵的各个数字，当子矩阵和为负数时，\(K_{i,j}\) 取 −1；子矩阵和为正数时，\(K_{i,j}\) 取 1。
  
  
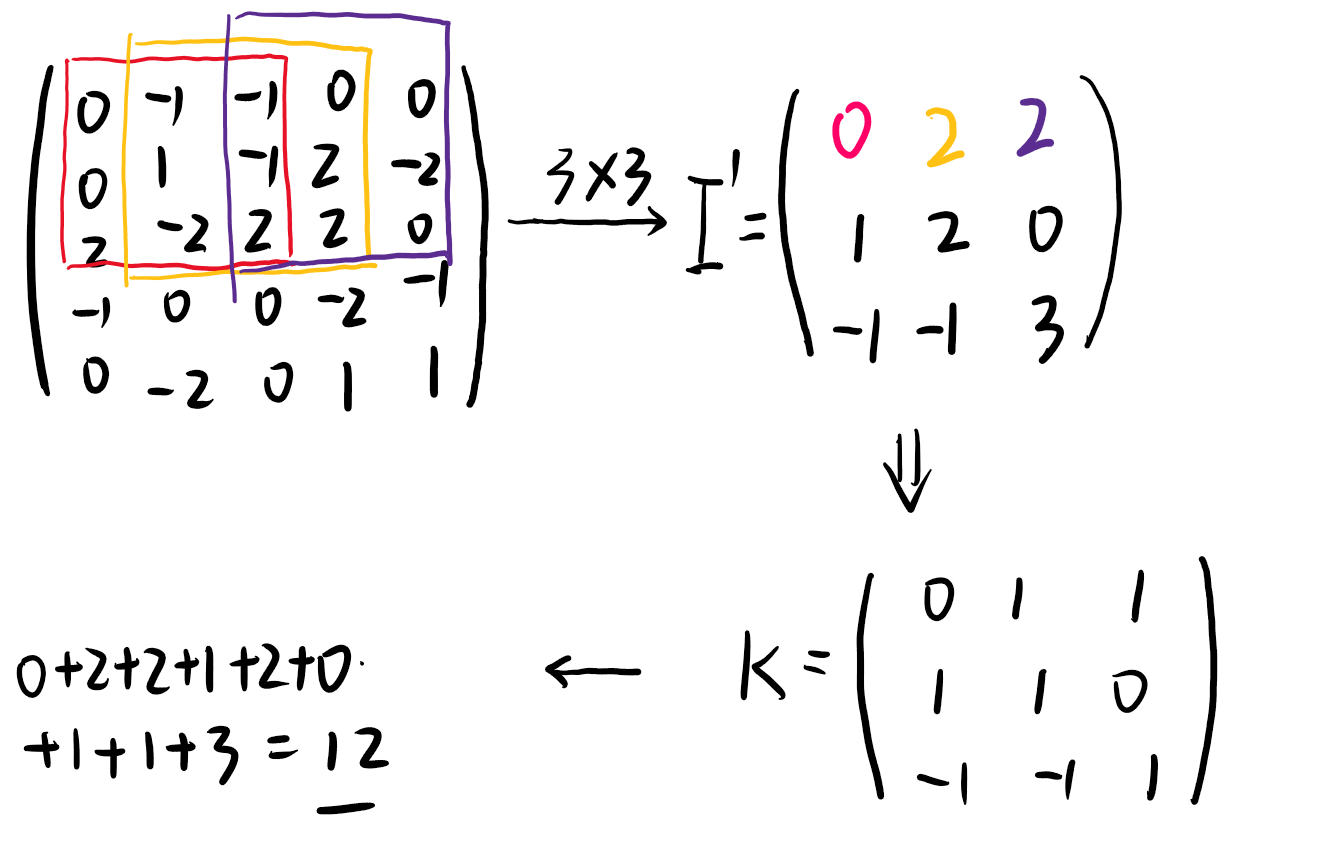
• 而根据上述分析，我们所需要计算的最终答案也就等于每个子矩阵各元素的绝对值之和。
• 快速求出某个子矩阵和可以用二维前缀和来实现。
• 值得注意的一点是使用cin和cout时为了提高效率记得要解除输入输出流的绑定（否则这道题可能会超时哦）。

Personal Solution

#include<bits/stdc++.h>
using namespace std;
long long num[1005][1005]={0};
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int n,m,k,l;
    cin>>n>>m>>k>>l;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>num[i][j];
            num[i][j]=num[i][j-1]+num[i][j]+num[i-1][j]-num[i-1][j-1];
        }
    }
    long long ct=0;
    for(int i=1;i<=k;i++){
        for(int j=1;j<=l;j++){
            ct=ct+abs(num[n-k+i][m-l+j]-num[n-k+i][j-1]-num[i-1][m-l+j]+num[i-1][j-1]);
        }
    }
    cout<<ct<<endl;
    return 0;
}