TensorFlow+Keras 02 深度学习的原理

1 神经传递的原理

人类的神经元传递及其作用：

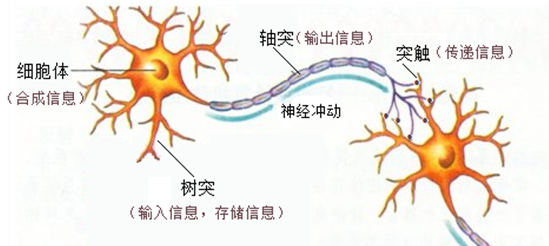
这里有几个关键概念：

• 树突 - 接受信息
• 轴突 - 输出信息
• 突触 - 传递信息

将其延伸到神经元中，示意图如下：

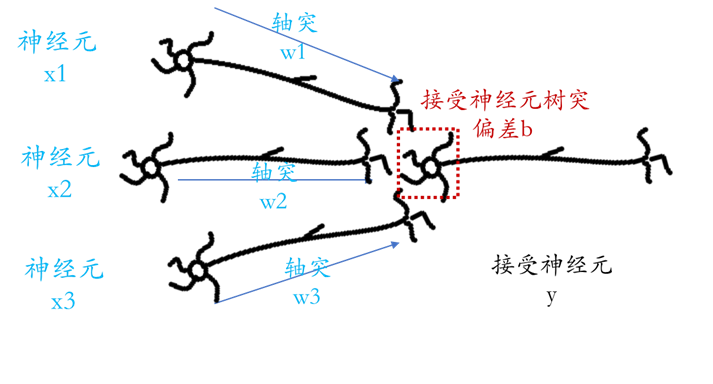
将上图整理成数学公式，则有

y = activation function( x1*w1 + x2*w2 + x3*w3 + b )

相应说明：

• x - 输入值，仿真输入神经元，上图中有：x1、x2、x3
• w - 权重值，仿真输入神经元轴突，传送信息，上图中有：w1、w2、w3
• b - 偏差值，仿真接受神经元树突，代表接受神经元容易被活化的程度，偏差值越高、越容易被激活，上图中接受神经元只有一个，所以也只有一个偏差值b。
• y - 通过一些列信息传导（激活函数运算），最终接受神经元所得到的值，也可以理解为输入神经元 x 有效传递了多少值
• 激活函数 - activation function ，仿真神经传递的工作方式，当接受神经元接收到刺激的总和（x1*w1 + x2*w2 + x3*w3 + b）经过激活函数的运算后，其值大于临界值时，就会传递至下一个神经元，常见的激活函数如Sigmoid、ReLU。

Sigmoid 激活函数

激活函数通常为非线性函数，其可仿真神经传导的工作方式将上一层神经元信号传递到下一层中。

TensorFlow 和 Keras 支持很多激活函数，常用的有两种：Sigmoid 和 ReLU。

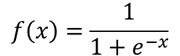
函数图像如下：

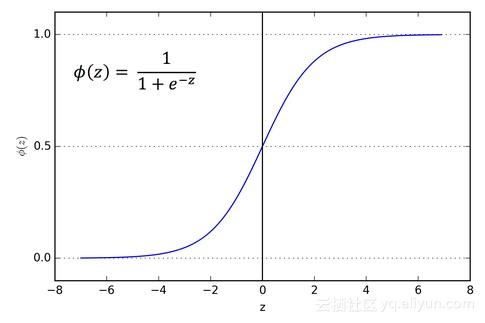
Sigmoid 激活函数类似于人类感觉神经：

• 小于临界值时，刺激被被忽略
• 大于临界值时，刺激会被接受
• 达到一定程度时，感觉会钝化，即使接受更大的刺激，感觉仍维持不变，如上图中为一条直线。

ReLU 激活函数

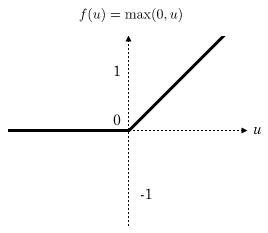
对比人类神经网络，可理解为：

• 小于临界值时，刺激会被忽略
• 大于临界值时，刺激被接受

2 以矩阵运算仿真神经网络

实际的神经网络存在有较多的值，此时一般用矩阵表示。

y = activation(x * w +b )

• x - 输入值，矩阵
• w - 权重值，矩阵
• b - 偏差值，矩阵
• y - 计算结果，矩阵

3 多层感知器模型

多层感知器（Multilayar Perceptron ，MLP）模型是一种受欢迎的及其学习解决方案，尤其是在语音识别、图像识别、和机器翻译等多个领域；20世纪90年代，MLP模型遭遇到更简单模型（如支持向量机SVM）的强烈竞争，近年来，由于深度学习的成功，MLP模型又重新收到业界重视。

以多层感知器模型识别MNIST手写数字图像为例，一般有

• 输入层 input layer
• 隐藏层 hidden layer
• 输出层 output layer

建立输入层与隐藏层的映射关系公式：h1 = ReLU ( x * w1 + b1 )

建立隐藏层与输出层的映射关系公式：y = softmax ( h1 * w2 + b2 )

4 使用反向传播算法进行训练

反向传播（Back Propagation）是训练人工神经网络的常见方法，且与优化器（Optimizer，如梯度下降法）结合使用。

反向传播是一种有监督的学习方法，必须有特征值features 和 标签 label

4.1 训练前必须先进行 ” 数据预处理 “ 和 ” 建立模型 “

4.1.1 数据预处理

MNIST 数据集经过数据预处理产生 数字图像特征值features和图像标签 label；备用。

4.1.2 建立模型

建立多层感知模型，并以随机数初始化模型的权重weight 和偏差值 bias。

4.2 反向传播算法训练多层感知器模型

进行训练时，数据分多批次喂入（如每次200项数据）进行模型训练；重复传播以使权重更新（ weight update )，直到误差 bias 收敛。

4.2.1 传播

1 - 向模型中喂入数据

2 - 模型输出计算结果

4.2.2 权重更新

1 - 损失函数计算误差。使用损失函数计算模型输出结果（预测结果）与 Label 标签之间的误差值

2 - 优化器更新权重与偏差。基于误差值更新权重和偏差，以使损失函数的误差值最小化。

4.3 损失函数

损失函数来帮助我们计算误差，其中 Cross Entropy 是深度学习常用的损失函数。

4.4 优化器

优化器是使用某种数值方法在不断的批次训练中不断更新权重与偏差，是损失函数的误差值最小化，并最终找到误差值最小的 ” 权重与偏差的组合 "。

在深度学习中，常用随机梯度下降法（Stochastic Gradient Descent ， SGD）来优化权重和偏差。

另外，还有许多随机梯度下降法的变形，如 RMSprop、Adagrad、Adadelta、Adam 等，这些适用于不同的深度学习模型，

5 附件：不同的优化器具有不同的训练效果图

Alec Radford's animations for optimization algorithms（Alec Radford的优化算法动画）

地址：http://www.denizyuret.com/2015/03/alec-radfords-animations-for.html

原文摘录：

Alec Radford创建了一些伟大的动画，比较优化算法SGD，Momentum，NAG，Adagrad，Adadelta，RMSprop（不幸的是没有Adam）的低维问题。另请查看他关于RNN的演讲。

Alec Radford has created some great animations comparing optimization algorithms SGD, Momentum, NAG, Adagrad, Adadelta, RMSprop(unfortunately no Adam) on low dimensional problems. Also check out his presentation on RNNs.

“ 嘈杂的卫星：这是来自sklearn的嘈杂卫星数据集的逻辑回归，它显示了基于动量的技术的平滑效果（这也导致过度射击和校正）。误差表面在经验上可视化为整个数据集的平均值，但是轨迹显示了微型数据在噪声数据上的动态。下图是精确度图。“

"Noisy moons: This is logistic regression on noisy moons dataset from sklearn which shows the smoothing effects of momentum based techniques (which also results in over shooting and correction). The error surface is visualized as an average over the whole dataset empirically, but the trajectories show the dynamics of minibatches on noisy data. The bottom chart is an accuracy plot."

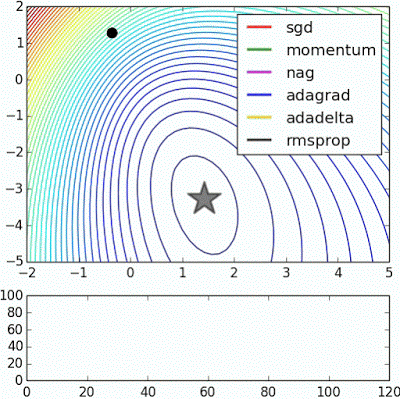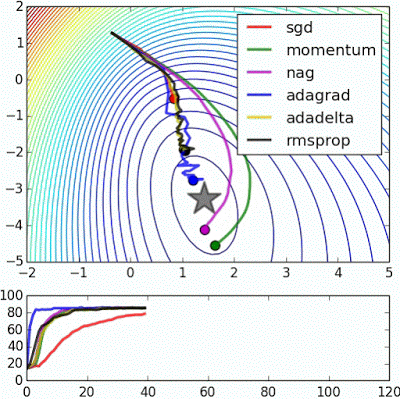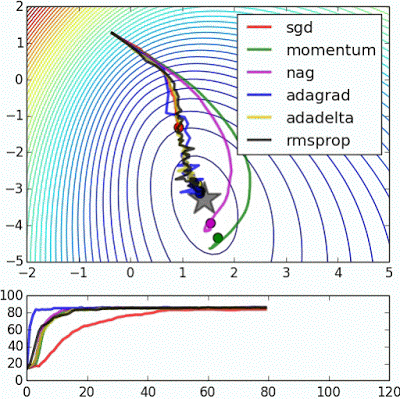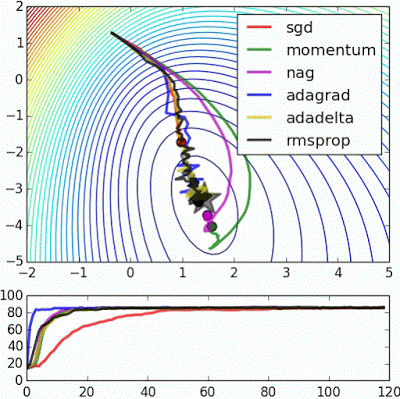
“ Beale的功能：由于大的初始梯度，基于速度的技术射击和反弹 - adagrad几乎变得不稳定，出于同样的原因。像adadelta和RMSProp那样缩放渐变/步长的算法更像加速SGD并处理大的渐变更稳定。“

"Beale's function: Due to the large initial gradient, velocity based techniques shoot off and bounce around - adagrad almost goes unstable for the same reason. Algos that scale gradients/step sizes like adadelta and RMSProp proceed more like accelerated SGD and handle large gradients with more stability."

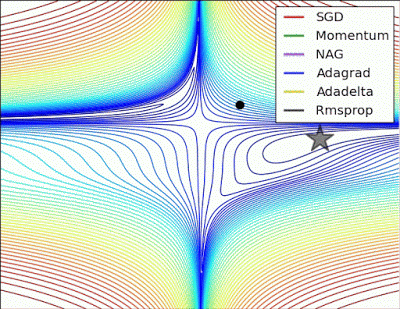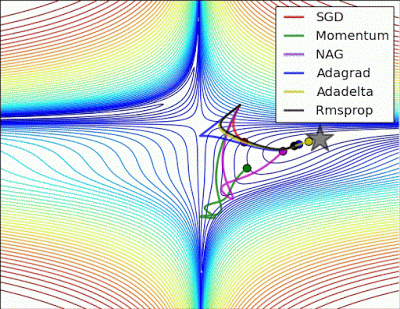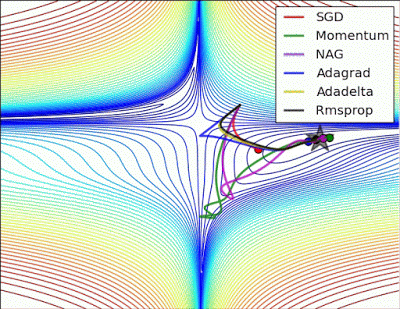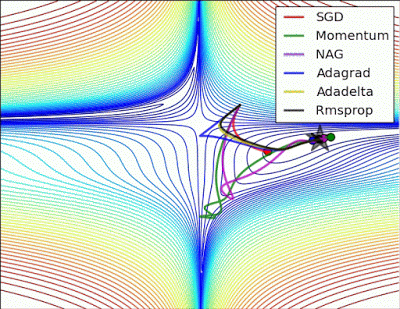
“ 长谷：没有根据梯度信息进行缩放的Algos在这里很难打破对称性 - SGD没有在哪里和Nesterov加速梯度/动量呈现振荡，直到它们在优化方向上建立速度。阿尔戈斯基于梯度快速缩放步长打破对称并开始下降。“

"Long valley: Algos without scaling based on gradient information really struggle to break symmetry here - SGD gets no where and Nesterov Accelerated Gradient / Momentum exhibits oscillations until they build up velocity in the optimization direction. Algos that scale step size based on the gradient quickly break symmetry and begin descent."

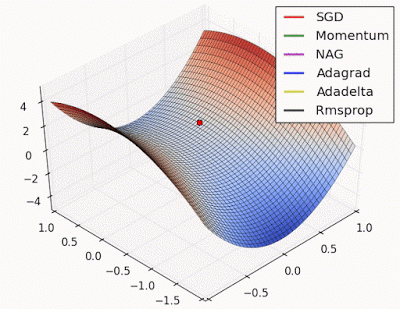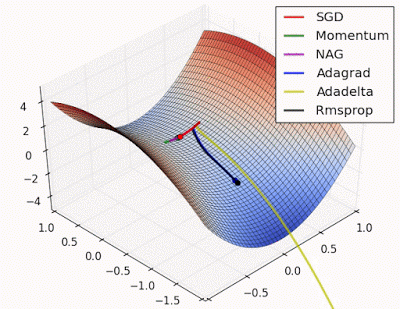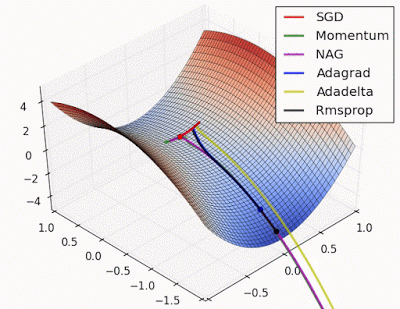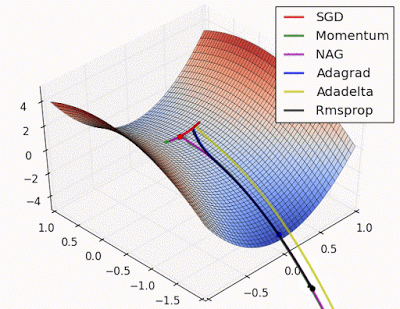
“ 鞍点：围绕鞍点的行为.NAG / Momentum再次喜欢探索周围，几乎采取不同的路径.Adadelta / Adagrad / RMSProp像加速SGD一样前进。”

"Saddle point: Behavior around a saddle point. NAG/Momentum again like to explore around, almost taking a different path. Adadelta/Adagrad/RMSProp proceed like accelerated SGD."