算法Sedgewick第四版-第1章基础-2.1Elementary Sortss-001选择排序法(Selection sort)

一、介绍

1.算法的时间和空间间复杂度

2.特点

Running time is insensitive to input. The process of finding the smallest item on one
pass through the array does not give much information about where the smallest item
might be on the next pass. This property can be disadvantageous in some situations.
For example, the person using the sort client might be surprised to realize that it takes
about as long to run selection sort for an array that is already in order or for an array
with all keys equal as it does for a randomly-ordered array! As we shall see, other algo-
rithms are better able to take advantage of initial order in the input.
Data movement is minimal. Each of the N exchanges changes the value of two array
entries, so selection sort uses N exchanges—the number of array accesses is a linear
function of the array size. None of the other sorting algorithms that we consider have
this property (most involve linearithmic or quadratic growth).

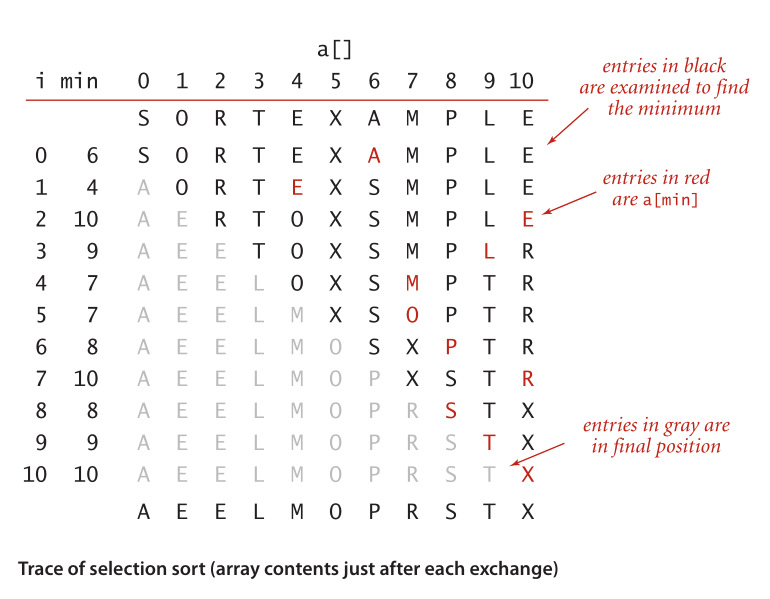
3.过程

二、代码

 package algorithms.elementary21;

 /******************************************************************************
  *  Compilation:  javac Selection.java
  *  Execution:    java  Selection < input.txt
  *  Dependencies: StdOut.java StdIn.java
  *  Data files:   http://algs4.cs.princeton.edu/21sort/tiny.txt
  *                http://algs4.cs.princeton.edu/21sort/words3.txt
  *
  *  Sorts a sequence of strings from standard input using selection sort.
  *
  *  % more tiny.txt
  *  S O R T E X A M P L E
  *
  *  % java Selection < tiny.txt
  *  A E E L M O P R S T X                 [ one string per line ]
  *
  *  % more words3.txt
  *  bed bug dad yes zoo ... all bad yet
  *
  *  % java Selection < words3.txt
  *  all bad bed bug dad ... yes yet zoo    [ one string per line ]
  *
  ******************************************************************************/

 import java.util.Comparator;

 import algorithms.util.StdIn;
 import algorithms.util.StdOut;

 /**
  *  The <tt>Selection</tt> class provides static methods for sorting an
  *  array using selection sort.
  *  <p>
  *  For additional documentation, see <a href="http://algs4.cs.princeton.edu/21elementary">Section 2.1</a> of
  *  <i>Algorithms, 4th Edition</i> by Robert Sedgewick and Kevin Wayne.
  *
  *  @author Robert Sedgewick
  *  @author Kevin Wayne
  */
 public class Selection {

     // This class should not be instantiated.
     private Selection() { }

     /**
      * Rearranges the array in ascending order, using the natural order.
      * @param a the array to be sorted
      */
     public static void sort(Comparable[] a) {
         int N = a.length;
         for (int i = 0; i < N; i++) {
             int min = i;
             for (int j = i+1; j < N; j++) {
                 if (less(a[j], a[min])) min = j;
             }
             exch(a, i, min);
             assert isSorted(a, 0, i);
         }
         assert isSorted(a);
     }

     /**
      * Rearranges the array in ascending order, using a comparator.
      * @param a the array
      * @param c the comparator specifying the order
      */
     public static void sort(Object[] a, Comparator c) {
         int N = a.length;
         for (int i = 0; i < N; i++) {
             int min = i;
             for (int j = i+1; j < N; j++) {
                 if (less(c, a[j], a[min])) min = j;
             }
             exch(a, i, min);
             assert isSorted(a, c, 0, i);
         }
         assert isSorted(a, c);
     }

    /***************************************************************************
     *  Helper sorting functions.
     ***************************************************************************/

     // is v < w ?
     private static boolean less(Comparable v, Comparable w) {
         return v.compareTo(w) < 0;
     }

     // is v < w ?
     private static boolean less(Comparator c, Object v, Object w) {
         return c.compare(v, w) < 0;
     }

     // exchange a[i] and a[j]
     private static void exch(Object[] a, int i, int j) {
         Object swap = a[i];
         a[i] = a[j];
         a[j] = swap;
     }

    /***************************************************************************
     *  Check if array is sorted - useful for debugging.
     ***************************************************************************/

     // is the array a[] sorted?
     private static boolean isSorted(Comparable[] a) {
         return isSorted(a, 0, a.length - 1);
     }

     // is the array sorted from a[lo] to a[hi]
     private static boolean isSorted(Comparable[] a, int lo, int hi) {
         for (int i = lo + 1; i <= hi; i++)
             if (less(a[i], a[i-1])) return false;
         return true;
     }

     // is the array a[] sorted?
     private static boolean isSorted(Object[] a, Comparator c) {
         return isSorted(a, c, 0, a.length - 1);
     }

     // is the array sorted from a[lo] to a[hi]
     private static boolean isSorted(Object[] a, Comparator c, int lo, int hi) {
         for (int i = lo + 1; i <= hi; i++)
             if (less(c, a[i], a[i-1])) return false;
         return true;
     }

     // print array to standard output
     private static void show(Comparable[] a) {
         for (int i = 0; i < a.length; i++) {
             StdOut.println(a[i]);
         }
     }

     /**
      * Reads in a sequence of strings from standard input; selection sorts them;
      * and prints them to standard output in ascending order.
      */
     public static void main(String[] args) {
         String[] a = StdIn.readAllStrings();
         Selection.sort(a);
         show(a);
     }
 }