牛客练习赛22-E.简单数据结构1（扩展欧拉定理降幂 +树状数组）

链接：E.简单数据结构1

题意：

给一个长为n的序列，m次操作，每次操作：

1.区间加

2.对于区间，查询 ，一直到-

请注意每次的模数不同。

 

题解：扩展欧拉定理降幂

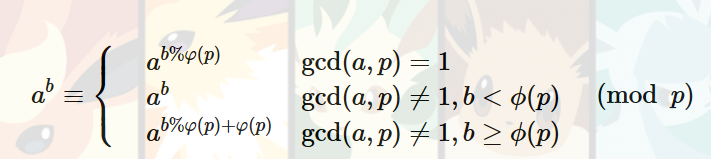
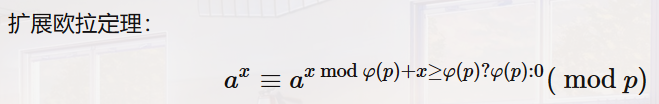
对一个数p取log(p)次的欧拉函数等于1，故可将操作2的复杂度降到log(p)，可以直接求解。用树状数组的小技巧，可以在log的时间直接求出当前的a[i]。具体见代码。

#include <bits/stdc++.h>
using namespace std;
 
const double EPS = 1e-;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + ;
const int maxn = 5e5 + ;
const int maxm = 2e7 + ;
int n, m;
long long a[maxn], bit[maxn];
int phi[maxm];
 
void Eul_list(int n)    //欧拉函数_list
{
    memset(phi, , sizeof(phi));
    phi[] = ;
 
    for(int i = ; i < n; i++){
        if(!phi[i]){
            for(int j = i; j < n; j += i){
                if(!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - );
            }
        }
    }
}
 
void add(int i, long long d)
{
    while(i < maxn){
        bit[i] += d;
        i += -i & i;
    }
}
 
long long sum(int i)
{
    long long ans = ;
    while(i){
        ans += bit[i];
        i -= -i & i;
    }
    return ans;
}
 
long long Mod(long long x, long long y)     //欧拉定理的条件
{
    return x < y ? x : x % y + y;
}
 
long long pow_mod(long long x, long long n, long long mod)
{
    long long ans = ;
    x = Mod(x, mod);
    while(n){
        if(n & ) ans = Mod(ans * x, mod);
        x = Mod(x * x, mod);
        n >>= ;
    }
    return ans;
}
 
long long dfs(int l, int r, int p)
{
    long long val = sum(l);
    if(l == r || p == ) return Mod(val, p);    //降幂加速
    return pow_mod(val, dfs(l + , r, phi[p]), p);
}
 
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = ; i <= n; i++){
        scanf("%lld", &a[i]);
        add(i, a[i] - a[i-]);      //对i求前缀和及为a[i]
    }
 
    Eul_list(maxm);
 
    int op, l, r, x;
    while(m--){
        scanf("%d%d%d%d", &op, &l, &r, &x);
        if(op == ){
            //只需要当前数时的更新技巧
            add(l, x);
            add(r + , -x);
        }
        else printf("%lld\n", dfs(l, r, x) % x);
    }
 
    return ;
}