[zoj] 1081 Points Within || 判断点是否在多边形内

原题

多组数据。

n为多边形顶点数，m为要判断的点数

按逆时针序给出多边形的点，判断点是否在多边形内，在的话输出"Within"，否则输出"Outside"

//每次要输出“Problem %d:"数据组数；

---

射线法

过要判断的点向x轴正方向做一条射线，如果交点数是奇数即在其中，否则不在其中。

枚举每条边，判断该点和边是否有交点。

若有交点，则：满足图一或图二之一（要保证y值在范围内）



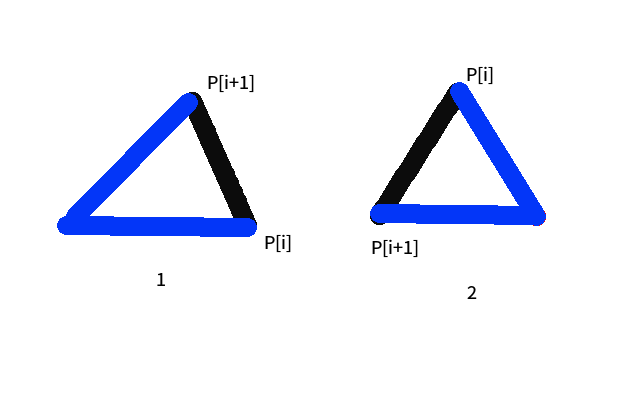
//因为按逆时针扫描顶点，所以第一种情况叉积>0；第二种<0

点是否在线段上特判即可（叉积=0，点积<=0）

area等是用于将点按逆时针存储，这道题其实据说不用

#include<cstdio>
#include<algorithm>
#define N 110
using namespace std;
int n,m,t;
struct point
{
    int x,y;
    point() {}
    point(int _x,int _y) : x(_x),y(_y) {}
    friend inline point operator - (const point &a,const point &b)
	{
	    return point(b.x-a.x,b.y-a.y);
	}
    friend inline int operator * (const point &a,const point &b)
	{
	    return a.x*b.y-a.y*b.x;
	}
    friend inline int dot(const point &a,const point &b)
	{
	    return a.x*b.x+a.y*b.y;
	}
}q;

inline int read()
{
    int ans=0,fu=1;
    char j=getchar();
    for (;j<'0' || j>'9';j=getchar()) if (j=='-') fu=-1;
    for (;j>='0' && j<='9';j=getchar()) ans*=10,ans+=j-'0';
    return ans*fu;
}

inline bool check(const point &u,const point &v,const point &p)
{
    int det=(u-p)*(v-p);
    if (det!=0) return 0;
    int Dot=dot(u-p,v-p);
    return Dot<=0;
}

struct polygon//(多边形)
{
    int n;
    point p[N];
    void init(int _n)
    {
	n=_n;
	for (int i=0;i<n;i++) { p[i].x=read(); p[i].y=read(); }
	p[n]=p[0];
	if (area()<0) reverse(p,p+n);
	p[n]=p[0];
    }
    inline int area() const//calc the area of polygon
    {
	int ret=0;
	for (int i=0;i<n;i++)
	    ret+=p[i]*p[i+1];
	return ret;
    }
    bool inner(const point &b)
    {
	int cnt=0;
	for (int i=0;i<n;i++)
	{
	    if (check(p[i],p[i+1],b)) return 1;
	    int d1=p[i].y-b.y,d2=p[i+1].y-b.y;
	    int det=(p[i]-b)*(p[i+1]-b);
	    if ((det>=0 && d1<0 && d2>=0) || (det<=0 && d1>=0 && d2<0))
	    ++cnt;
	}
	return cnt&1;
    }
}P;

int main()
{
    while (~scanf("%d",&n) && n)
    {
	m=read();
	if (t) putchar('\n');
	P.init(n);
	printf("Problem %d:\n",++t);
	while (m--)
	{
	    q.x=read();
	    q.y=read();
	    if (P.inner(q)) puts("Within");
	    else puts("Outside");
	}
    }
    return 0;
}