2016011998+sw

Coding.net原码仓库地址：https://git.coding.net/laolaf/sw.git

目录

1 需求分析

2 功能设计

3 设计实现

4 算法详解

5 测试运行

6 满意代码

1 需求分析

用户分析：本软件的用户是小学生，因此，要对数据和算式进行限定。
限定条件总结如下：

1 数据是不超过1000的正整数；

2 运算符在3到5个之间；

3 运算过程中不能产生负数或分数（基本功能中）。

本软件具有以下功能：

1 接受参数n后可自动生成n道至少包含2种运算符的练习题，且不出现非整数或负数。

2 生成练习题后，学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中。

3 在拓展类进行复杂真分数运算。

2 功能设计：

基本功能：随机生成只有正整数的四则运算算式和答案。

扩展功能：a 支持有括号的运算式，包括出题与求解正确答案。算式中存在的括号必须大于2个，且不得超过运算符的个数。

b   扩展程序功能支持真分数的出题与运算，例如：1/6 + 1/8 + 2/3= 23/24。实现本功能时，支持运算时分数的自动化简。

模块设计：

1 Cal方法：用于转化字符串并计算得到的算式的值，支持括号运算。

2 Create方法：用于生成符合要求的算式的字符串形式。

3 Add方法：支持真分数运算的模块 。

4 main方法：输出

3 设计实现：

本软件的类：Main。主要用到了2个方法。可完成以下功能：

1. 基本四则运算：功能由Cal和Create完成，由Create产生合法的（运算中不出现负数和分数）的算式，再利用Cal计算。
2. 加括号的四则运算：没做。

方法：

1 Cal(String str)：实现计算一个多运算符的算式。参数str即是要进行运算的字符串。在算法详解中会提到。

2 CreateQuestion(int p)：实现创造一个合法的算式。参数p是运算符号的个数。

它的主体：

 public static String CreateQuestion(int p) {// 产生1个包含p个运算符的四则运算的方法
               String re = "";//result

               char oper[]={'+','-','*','÷'};//operator
               int Num[]=new int[30];//存储算式中的运算数
               char Op[]=new char[30];//xxxxxx    运算符  

                   for(int he=p;he>0;he--){
                       Op[he]=oper[(int) (Math.random()*4)];
                   }

                   for(int he=p+1;he>0;he--){
                       Num[he]=(int) (Math.random()*100);
                   } 

                   //谢绝野蛮连成连÷
                   for(int e=p;e>0;e--){
                       if(Op[e]=='*'||Op[e]=='÷')
                           while(Op[e]!='*'&&Op[e]!='÷')
                               Op[1+e]=oper[(int) (Math.random()*4)];
                   }

                   //合法性问题：1 负数  2 分数.
                   //先对乘除处理，处理之后，归纳为简单加减运算'

                   /* 解决分数问题          */
                   for(int e=p;e>0;e--){
                       if(Op[e]=='÷') Num[e-1]*=Num[e+1]; 

                   }

                   /*控制fu数问题，先计算已经产生的字符串，控制减数永远比被减数小，同时注意减数不能小于o*/
                   for(int e=0;e<p;e++){
                         if(Op[e] == '-')
                           {
                               String Caled= "" + Num[0];
                               for(int c=0; c<p; c++)
                                   Caled= Caled + Op[c] + Op[c+1];
                              int existed = Cal(Caled);
                              Num[e+1] = existed-(int) (Math.random()*existed);
                           };

                   }

                 re=re+Num[0];
                for(int pp=0;pp<p;pp++)
                    re=re+Op[pp]+Num[pp+1];
                return re;//返回一个合法的算式

         }

4 算法详解

用到的主要算法是逆波兰表达式和调度场算法---用来计算字符串状态下算式的值。

参考了链接：https://liam0205.me/2016/12/14/Shunting-Yard-Algorithm/]

这里讲得很清楚了：

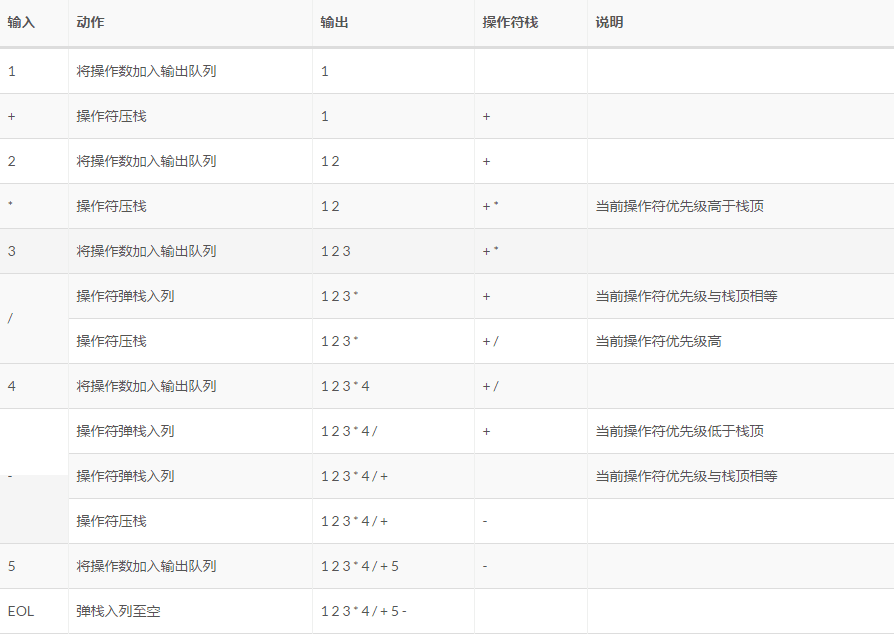
简单地说，就是先将要输入的表达式存入list中，然后，将表达式变为逆波兰表达式压入栈内，通过正则判断字符串是否为数字，是，输出到集合里，不是，则进行优先级的判断，括号的级别最高，其次是乘除，然后是加减。

部分代码：

 List<String> list = (List<String>) new ArrayList<>();
        Collections.addAll(list, expression);

        Stack<String> stack = new Stack<>();

        List<String> RPNList = new ArrayList<>();

        String numRegex = "^-?[0-9]+$";

        for(String s : list) {
            if(s.matches(numRegex)) {

                RPNList.add(s);
            }else if("*".equals(s) || "/".equals(s) || "+".equals(s) || "-".equals(s)) {

                if(stack.isEmpty()) {
                    stack.push(s);
                }else{
                    int currLevel = getLevel(s);
                    String topStr = stack.peek();
                    int topLevel = getLevel(topStr);
                    if (currLevel <= topLevel) {
                        // 栈顶元素依次出栈并输出
                        while(!stack.isEmpty()) {
                            // 遇到左括号退出
                            String peek = stack.peek();
                            if("(".equals(peek)) {
                                break;
                            }
                            RPNList.add(stack.pop());
                        }
                    }
                    stack.push(s);
                }
            }else if("(".equals(s)) {
                stack.push(s);
            }else if(")".equals(s)) {
                // 栈顶元素依次出栈并输出
                int length = stack.size();
                for(int i = 0; i < length; i++) {
                    String pop = stack.pop();
                    // 遇到左括号退出 并丢弃“”"("
                    if("(".equals(pop)) {
                        break;
                    }
                    RPNList.add(pop);
                }
            }
        }
        // 如果栈中还有元素 弹出
        if(!stack.isEmpty()) {
            // 栈顶元素依次出栈并输出
            int length = stack.size();
            for(int i = 0; i < length; i++) {
                RPNList.add(stack.pop());
            }
        }
     

5 测试运行

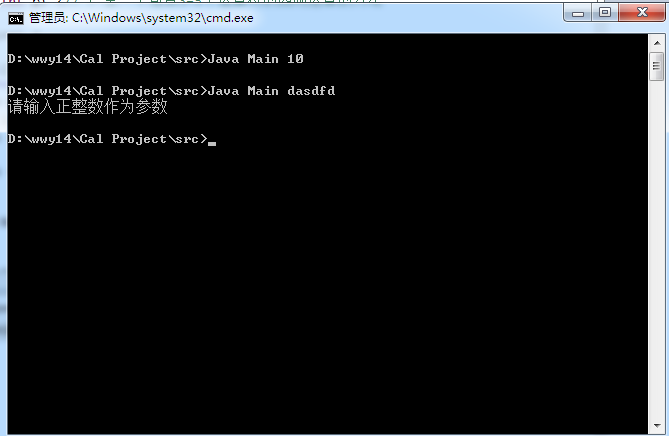
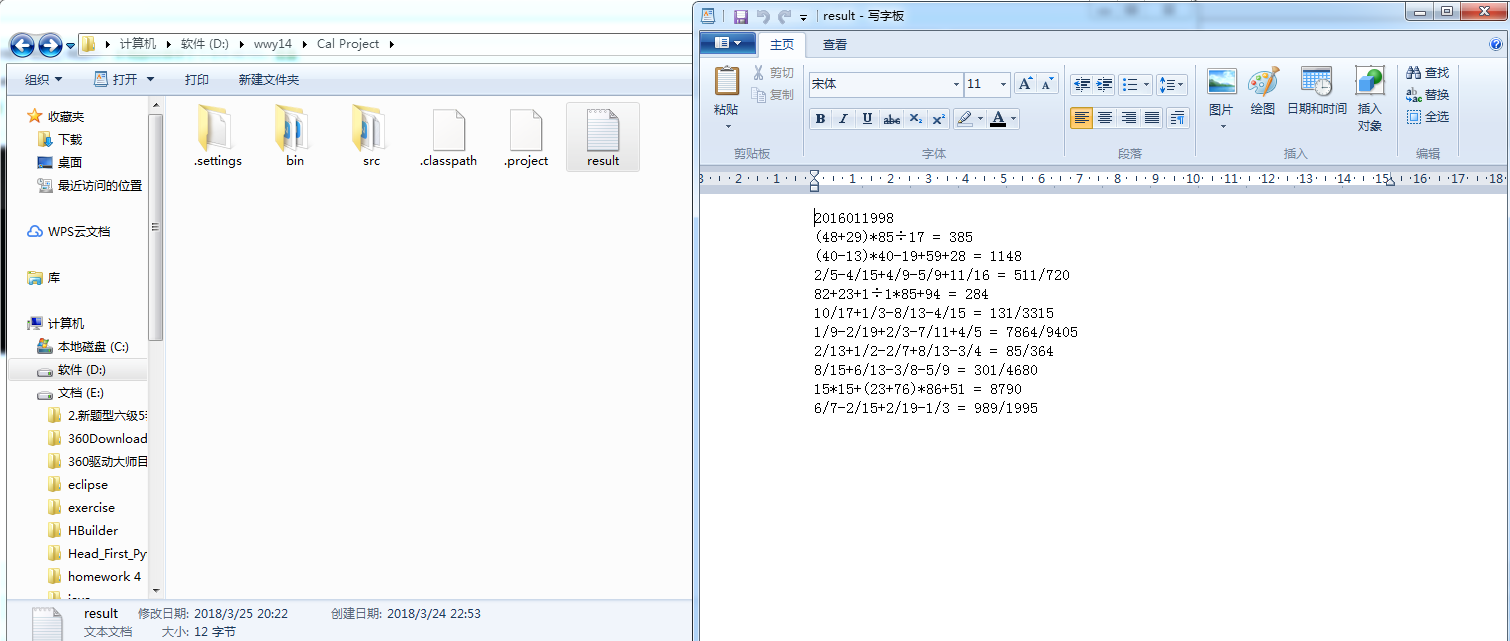
6 满意的代码：

在对算式的合法性进行控制时，对除法的控制：

 //谢绝野蛮连成连÷
            for(int e=0;e<p;e++){
                if(Op[e]=='*'||Op[e]=='÷')
                   Op[1+e]=oper[(int) (Math.random()*2)];
                    if(Op[e]!='*'&&Op[e]!='÷')
                        Op[1+e]=oper[(int) (Math.random()*4)];
            }
            //sffg
            //合法性问题：1 负数  2 分数.
            //先对乘除处理，处理之后，归纳为简单加减运算'
            /* 解决分数问题          */
            for(int e=0;e<p;e++){
                if(Op[e]=='÷')
                    Num[e]=Num[e+1]*(int)(Math.random()*20);

                if(Op[e]=='-')
                {
                    Num[e+1]=(int)(Math.random()*Num[e]/8);
                   // Num[e+2]=(int)(Math.random()*Num[e+1]);
                    Num[e+2]=(int)(Math.random()*4)+1;

                }
            }

首先避免了连÷（以及连*---这是防止数据过大），可以减少判断。然后，对整个算式进行搜索，发现符号为÷的，将除号前的被除数字乘上除数，这样永远不会出现未除尽的情况。

7 总结：完成这次作业最大的障碍就是语言问题，对于java过于陌生了些。另外，我觉得这次的作业还是可以体现模块化原则的，虽然我把所有的方法都写道一个类里面去了，但是功能是由各个组件独立完成的。

8 psp

PSP2.1	任务内容	计划共完成需要的时间(h)	实际完成需要的时间(h)
Planning	计划	0.5	0.5
·        Estimate	·   估计这个任务需要多少时间，并规划大致工作步骤	0.5	0.5
Development	开发	40	58.5
·        Analysis	·         需求分析 (包括学习新技术)	10.5	30
·        Design Spec	·         生成设计文档	0.5	0.5
·        Design Review	·         设计复审 (和同事审核设计文档)	0	0
·        Coding Standard	·         代码规范 (为目前的开发制定合适的规范)	0.5	1
·        Design	·         具体设计	1	1.5
·        Coding	·         具体编码	18	21
·        Code Review	·         代码复审	1	2
·        Test	·         测试（自我测试，修改代码，提交修改）	1	1
Reporting	报告	3	2
·         Test Report	·         测试报告	0.5	0.5
·         Size Measurement	·         计算工作量	0	0
·         Postmortem & Process Improvement Plan	·         事后总结, 并提出过程改进计划	0.5	0.5