归并排序的理解和实现(Java)

归并排序介绍

归并排序(Merge Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有ｆn个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到[n2\frac{n}{2}2n​]（[x]表示不小于x的最小整数）个长度为2或1的有序子序列；在两两归并，…，如此重复，知道得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。

根据具体的实现，归并排序包括"从上往下"和"从下往上"2种方式。

下面的图片很清晰的反映了"从下往上"和"从上往下"的归并排序的区别。

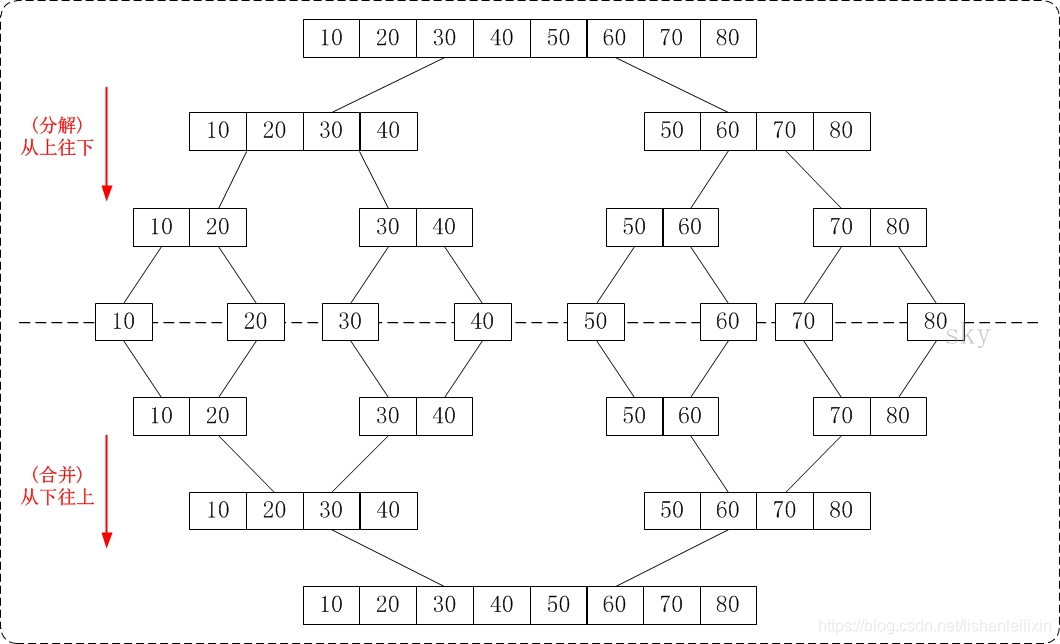
从上往下

代码实现：

	/**
	 * 从上到下
	 * @param elem
	 * @param start
	 * @param end
	 */
	public void mergeSortUp2Down(int[] elem, int start, int end) {
		if(elem == null || start >= end) {
			return;
		}
		int mid = (start + end) / 2;
		mergeSortUp2Down(elem, start, mid);
		mergeSortUp2Down(elem, mid + 1, end);
		merge(elem, start, mid, end);
	}
	public void merge(int[] elem, int start, int mid, int end) {
		int[] temp = new int[end - start + 1];
		int i = start;
		int j = mid + 1;
		int k = 0;
		while(i <= mid && j <= end) {
			if(elem[i] < elem[j]) {
				temp[k++] = elem[i++];
			}
			else {
				temp[k++] = elem[j++];
			}
		}
		while(i <= mid) {
			temp[k++] = elem[i++];
		}
		while(j <= end) {
			temp[k++] = elem[j++];
		}
		for (i = 0; i < k; i++) {
			elem[start + i] = temp[i];
		}
		temp = null;
	}

从上往下的思路如图所示：

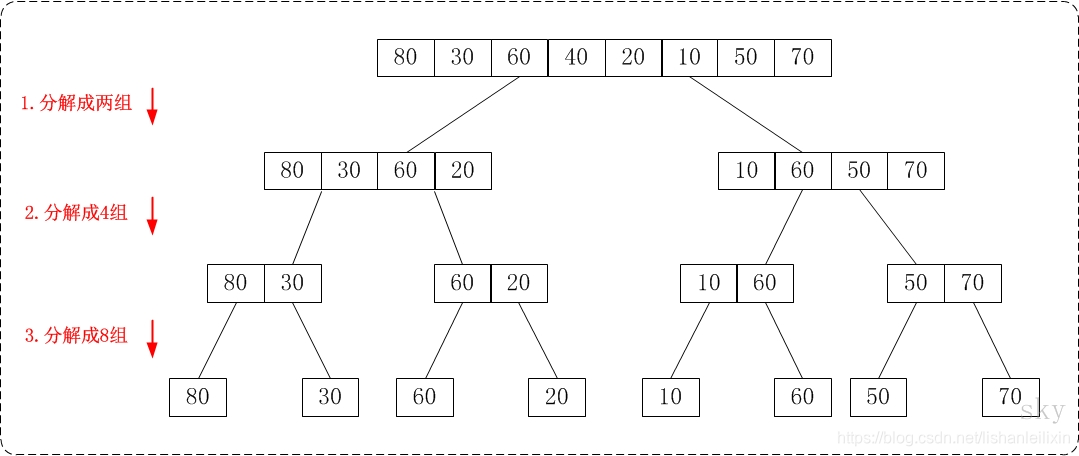
从下往上

代码实现：

	/**
	 * 从下到上
	 * @param elem
	 */
	public void mergeSortDown2Up(int[] elem) {
		if(elem == null) return;
		for (int i = 1; i < elem.length; i *= 2) {
			mergeGroups(elem, elem.length, i);
		}
	}
	public void mergeGroups(int[] elem, int len, int gap) {
		int i;
		for (i = 0; i + 2 * gap -1 < len; i += (2 * gap)) {
			merge(elem, i, i + gap -1, i + 2 * gap -1);
		}
		if(i + gap -1 < len - 1) {
			merge(elem, i, i + gap - 1, len - 1);
		}
	}

归并排序的复杂度分析

归并排序的时间复杂度是O(nlog⁡\loglogn)。

假设被排序的数列中有n个元素。遍历一趟的时间复杂度是O(n)，需要遍历多少次呢？归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的性质可以得知可以得出它的时间复杂度是O(nlog⁡\loglogn)。

由于归并怕徐在归并过过程中需要与原始记录序列同样数量的存储空间存放归并结果以及递归时深度为log2log_2log2​n的栈空间，所以空间复杂度为O(n + log⁡\loglogn)

归并排序是稳定的算法，它满足稳定算法的定义。

归并排序的非递归实现

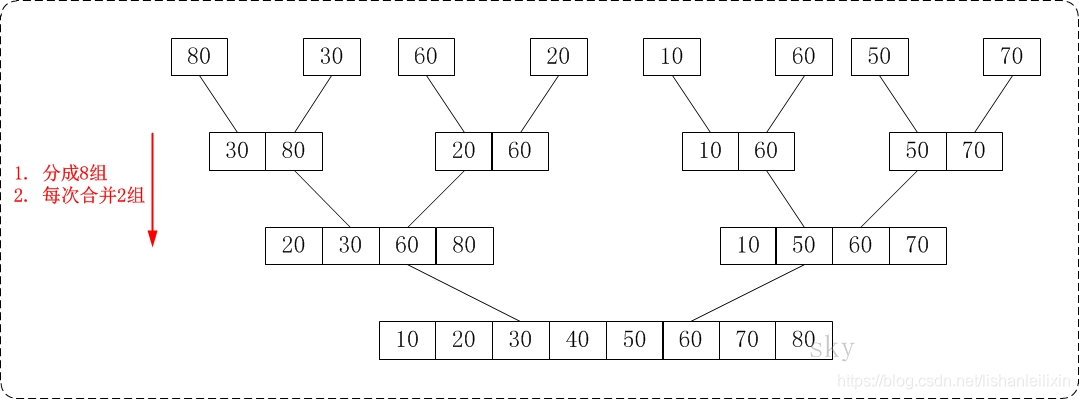
非递归的思想和递归一样，均为先分解后合并，非递归的重点在于如何确定并合理的分解待排序数组。

对于非递归来讲，切分的不向递归从大到小，非递归实际上从一开始构建算法的时候都从小到大。

第一次切分排序就确定最小单位为1个数字，将2个数字组合为一组。



第二次切分排序确定为2个数字，将4个数字组合为一组。



第三次切分排序确定为4个数字，将8（7）个数字组合为一组。



也就是说非递归归并排序中分解的依据为：从切分的长度为1开始，一次归并变回原来的2倍。每完成一次归并则 gap = gap * 2。

	/**
	 * 非递归
	 * @param elem
	 */
	public void mergeSortNon(int[] elem) {
		int gap = 1;
		while(gap <= elem.length) {
			for (int i = 0; i + gap < elem.length; i += (gap * 2)) {
				int start = i, mid = i + gap -1, end = i + 2 * gap -1;
				if(end > elem.length - 1) {
					end = elem.length - 1;
				}
				merge(elem, start, mid, end);
			}
			gap *= 2;
		}
	}

完整代码：

public class Test {
	/**
	 * 从上到下
	 * @param elem
	 * @param start
	 * @param end
	 */
	public void mergeSortUp2Down(int[] elem, int start, int end) {
		if(elem == null || start >= end) {
			return;
		}
		int mid = (start + end) / 2;
		mergeSortUp2Down(elem, start, mid);
		mergeSortUp2Down(elem, mid + 1, end);
		merge(elem, start, mid, end);
	}
	/**
	 * 从下到上
	 * @param elem
	 */
	public void mergeSortDown2Up(int[] elem) {
		if(elem == null) return;
		for (int i = 1; i < elem.length; i *= 2) {
			mergeGroups(elem, elem.length, i);
		}
	}
	public void mergeGroups(int[] elem, int len, int gap) {
		int i;
		for (i = 0; i + 2 * gap -1 < len; i += (2 * gap)) {
			merge(elem, i, i + gap -1, i + 2 * gap -1);
		}
		if(i + gap -1 < len - 1) {
			merge(elem, i, i + gap - 1, len - 1);
		}
	}
	/**
	 * 非递归
	 * @param elem
	 */
	public void mergeSortNon(int[] elem) {
		int gap = 1;
		while(gap <= elem.length) {
			for (int i = 0; i + gap < elem.length; i += (gap * 2)) {
				int start = i, mid = i + gap -1, end = i + 2 * gap -1;
				if(end > elem.length - 1) {
					end = elem.length - 1;
				}
				merge(elem, start, mid, end);
			}
			gap *= 2;
		}
	}
	public void merge(int[] elem, int start, int mid, int end) {
		int[] temp = new int[end - start + 1];
		int i = start;
		int j = mid + 1;
		int k = 0;
		while(i <= mid && j <= end) {
			if(elem[i] < elem[j]) {
				temp[k++] = elem[i++];
			}
			else {
				temp[k++] = elem[j++];
			}
		}
		while(i <= mid) {
			temp[k++] = elem[i++];
		}
		while(j <= end) {
			temp[k++] = elem[j++];
		}
		for (i = 0; i < k; i++) {
			elem[start + i] = temp[i];
		}
		temp = null;
	}
	public static void main(String[] args) {
		Test t = new Test();
		int[] elem = {80,30,60,40,20,10,50,70};
		t.mergeSortUp2Down(elem, 0, elem.length - 1); //从上到下
//		t.mergeSortDown2Up(elem); //从下到上
//		t.mergeSortNon(elem);  //非递归
		for (int i = 0; i < elem.length; i++) {
			System.out.print(elem[i] + ", ");
		}
	}
}

参考：

https://www.cnblogs.com/skywang12345/p/3602369.html

https://www.cnblogs.com/yulinfeng/p/7078661.html?utm_source=itdadao&utm_medium=referral

《大话数据结构》

补充说明

最近在做一道《剑指Offer》上的一道算法的时候，用到了归并排序，因此加深了我对归并排序的核心排序(merge())方法加深了理解：



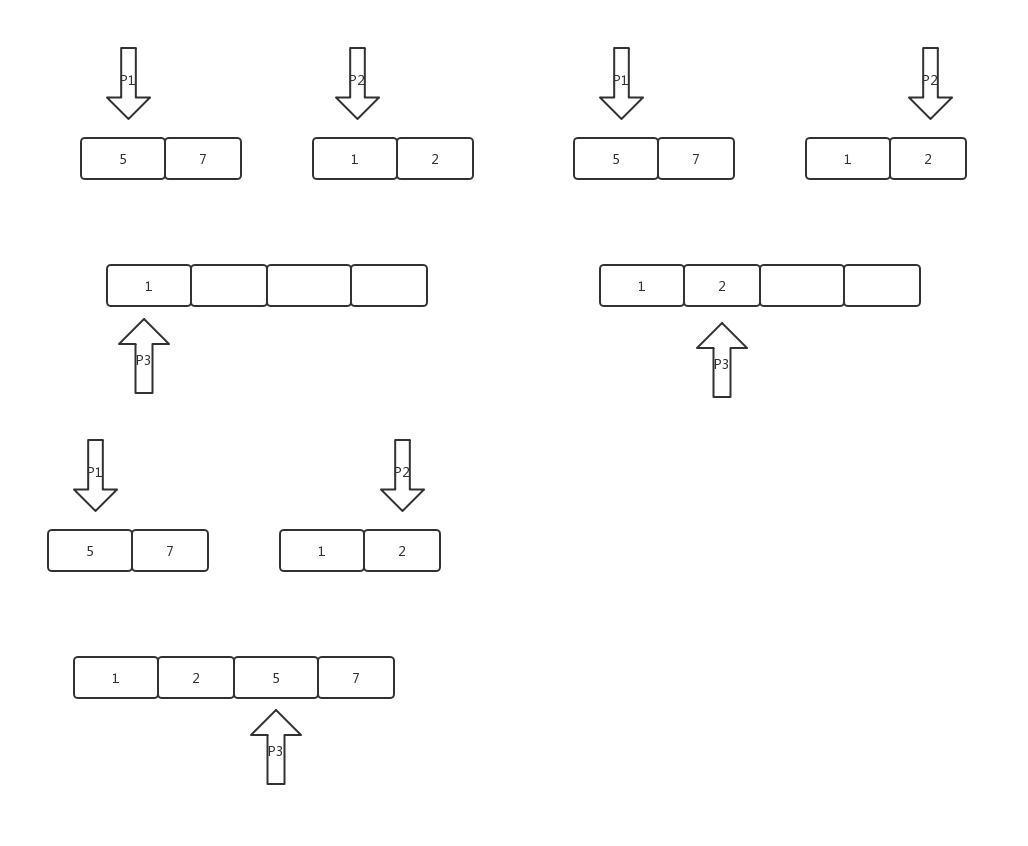
其实核心的排序就是设立三个指针P1, P2, P3。P3指针所指的数组就是两个数组合并且排序后的数组。每次比较P1和P2指针所指的元素：

• 如果P1<P2，那么将P1所指的元素赋给P3所指的数组节点，并将P1和P3的指针后移一位，P2指针不动。
• 如果P1>P2，那么将P2所指的元素赋给P3所指的数组节点，并将P2和P3的指针后移一位，P1指针不动。
• 当P1或P2其中某一个指针指到最后了，那么也就是说两个数组比较排序已经完成，但是其中一个数组还“剩下”一部分元素(注意剩下的这些元素是有序的且剩下元素中最小的元素也大于新数组的最大元素)，将剩下这部分的元素放在新数组后面。