Luogu P3384 【【模板】树链剖分】

转载请注明出处，部分内容引自banananana大神的博客

---

~~别说你不知道什么是树~~╮(─▽─)╭（帮你百度一下）

---

先来回顾两个问题：
1，将树从x到y结点最短路径上所有节点的值都加上z

这也是个模板题了吧

我们很容易想到，树上差分可以以O(n+m)的优秀复杂度解决这个问题

2，求树从x到y结点最短路径上所有节点的值之和

lca大水题，我们又很容易地想到，dfs O(n)预处理每个节点的dis（即到根节点的最短路径长度）

然后对于每个询问，求出x,y两点的lca，利用lca的性质distance ( x , y ) = dis ( x ) + dis ( y ) - 2 * dis ( lca )求出结果

时间复杂度O(mlogn+n)

现在来思考一个bug：
如果刚才的两个问题结合起来，成为一道题的两种操作呢？

刚才的方法显然就不够优秀了（每次询问之前要跑dfs更新dis）

---

树链剖分华丽登场
树剖是通过轻重边剖分将树分割成多条链，然后利用数据结构来维护这些链（本质上是一种优化暴力）

首先明确概念：

重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；

轻儿子：父亲节点中除了重儿子以外的儿子；

重边：父亲结点和重儿子连成的边；

轻边：父亲节点和轻儿子连成的边；

重链：由多条重边连接而成的路径；

轻链：由多条轻边连接而成的路径；

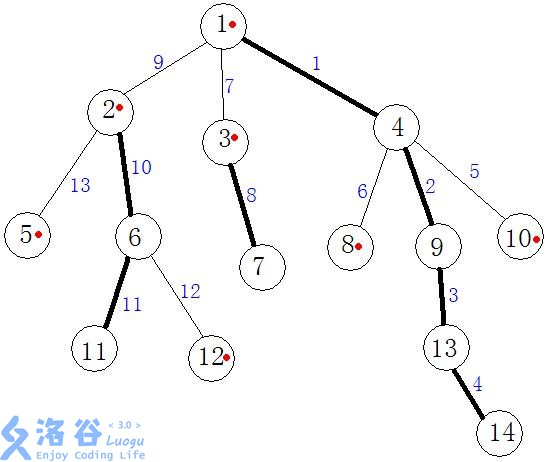
比如上面这幅图中，用黑线连接的结点都是重结点，其余均是轻结点，

2-11就是重链，2-5就是轻链，用红点标记的就是该结点所在重链的起点，也就是下文提到的top结点，

还有每条边的值其实是进行dfs时的执行序号。
变量声明：

const int maxn=1e5+10;
struct edge{
    int next,to;
}e[2*maxn];
struct Node{
    int sum,lazy,l,r,ls,rs;
}node[2*maxn];
int rt,n,m,r,a[maxn],cnt,head[maxn],f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],id[maxn];

名称	解释
f[u]	保存结点u的父亲节点
d[u]	保存结点u的深度值
size[u]	保存以u为根的子树节点个数
son[u]	保存重儿子
rk[u]	保存当前dfs标号在树中所对应的节点
top[u]	保存当前节点所在链的顶端节点
id[u]	保存树中每个节点剖分以后的新编号（DFS的执行顺序）

我们要做的就是（树链剖分的实现）：
1，对于一个点我们首先求出它所在的子树大小,找到它的重儿子（即处理出size,son数组），
解释:比如说点1，它有三个儿子2，3，4

2所在子树的大小是5

3所在子树的大小是2

4所在子树的大小是6

那么1的重儿子是4

ps:如果一个点的多个儿子所在子树大小相等且最大

那随便找一个当做它的重儿子就好了

叶节点没有重儿子，非叶节点有且只有一个重儿子
2，在dfs过程中顺便记录其父亲以及深度（即处理出f,d数组），操作1,2可以通过一遍dfs完成

void dfs1(int u,int fa,int depth)    //当前节点、父节点、层次深度
{
    f[u]=fa;
    d[u]=depth;
    size[u]=1;    //这个点本身size=1
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v==fa)
            continue;
        dfs1(v,u,depth+1);    //层次深度+1
        size[u]+=size[v];    //子节点的size已被处理，用它来更新父节点的size
        if(size[v]>size[son[u]])
            son[u]=v;    //选取size最大的作为重儿子
    }
}
//进入
dfs1(root,0,1);

dfs跑完大概是这样的，大家可以手动模拟一下
3，第二遍dfs，然后连接重链，同时标记每一个节点的dfs序，并且为了用数据结构来维护重链，我们在dfs时保证一条重链上各个节点dfs序连续（即处理出数组top,id,rk）

void dfs2(int u,int t)    //当前节点、重链顶端
{
    top[u]=t;
    id[u]=++cnt;    //标记dfs序
    rk[cnt]=u;    //序号cnt对应节点u
    if(!son[u])
        return;
    dfs2(son[u],t);
/*我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续，
一个点和它的重儿子处于同一条重链，所以重儿子所在重链的顶端还是t*/
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v!=son[u]&&v!=f[u])
            dfs2(v,v);    //一个点位于轻链底端，那么它的top必然是它本身
    }
}

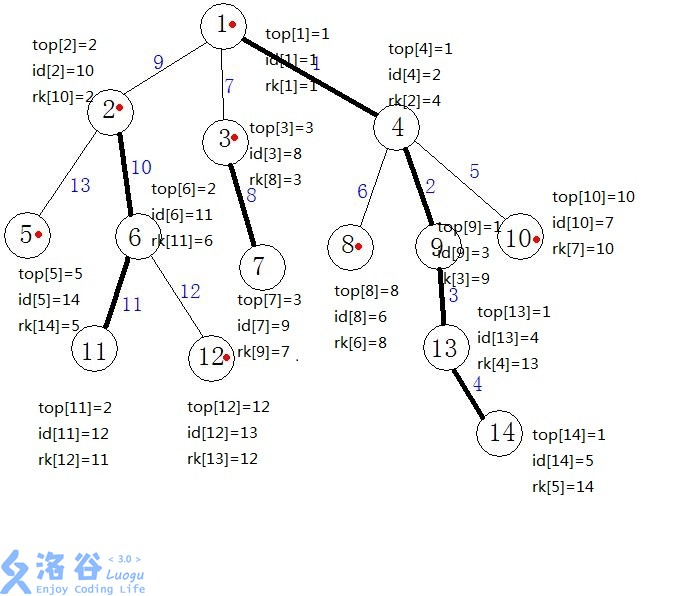
dfs跑完大概是这样的，大家可以手动模拟一下
4，两遍dfs就是树链剖分的主要处理，通过dfs我们已经保证一条重链上各个节点dfs序连续，那么可以想到，我们可以通过数据结构（以线段树为例）来维护一条重链的信息
回顾上文的那个题目，修改和查询操作原理是类似的，以查询操作为例，其实就是个LCA，不过这里使用了top来进行加速，因为top可以直接跳转到该重链的起始结点，轻链没有起始结点之说，他们的top就是自己。需要注意的是，每次循环只能跳一次，并且让结点深的那个来跳到top的位置，避免两个一起跳从而擦肩而过。

int sum(int x,int y)
{
    int ans=0,fx=top[x],fy=top[y];
    while(fx!=fy)    //两点不在同一条重链
    {
        if(d[fx]>=d[fy])
        {
            ans+=query(id[fx],id[x],rt);    //线段树区间求和，处理这条重链的贡献
            x=f[fx],fx=top[x];    //将x设置成原链头的父亲结点，走轻边，继续循环
        }
        else
        {
            ans+=query(id[fy],id[y],rt);
            y=f[fy],fy=top[y];
        }
    }
    //循环结束，两点位于同一重链上，但两点不一定为同一点，所以我们还要统计这两点之间的贡献
    if(id[x]<=id[y])
        ans+=query(id[x],id[y],rt);
    else
        ans+=query(id[y],id[x],rt);
    return ans;
}

大家如果明白了树链剖分，也应该有举一反三的能力（反正我没有），修改和LCA就留给大家自己完成了
5，树链剖分的时间复杂度
树链剖分的两个性质：

1，如果(u, v)是一条轻边，那么size(v) < size(u)/2；

2，从根结点到任意结点的路所经过的轻重链的个数必定都小于logn；

可以证明，树链剖分的时间复杂度为O(nlogn)
例题：
树链剖分模板
就是刚才讲的
上代码：