【清华集训 2017】小Y的地铁 [模拟退火]

小Y的地铁

Time Limit: 50 Sec  Memory Limit: 256 MB

Description

　

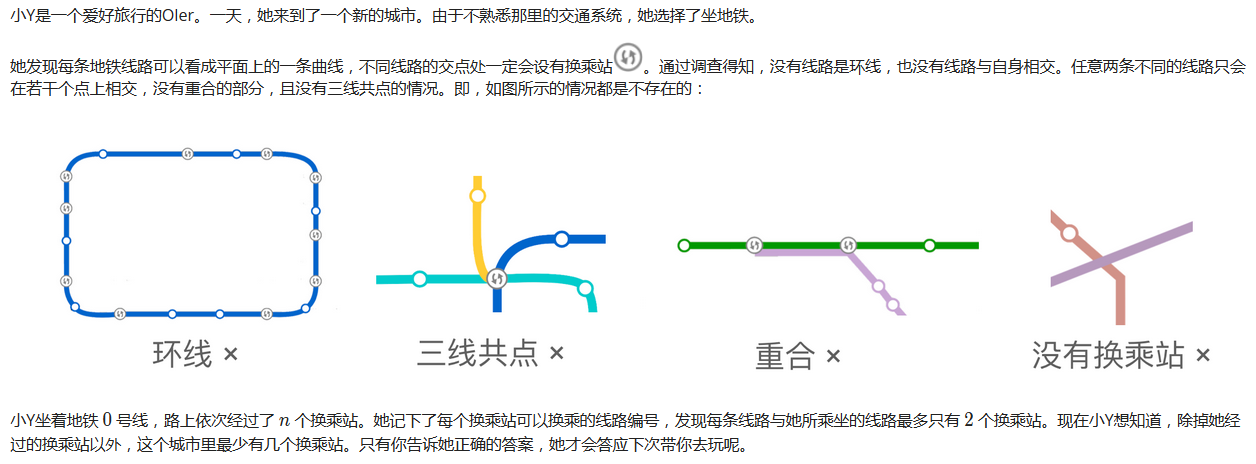
Input

　　

Output

　　对于每组输入数据，输出一行一个整数，表示除掉这 n 个换乘站之外，最少有几个换乘站。

Sample Input

　　4
　　4
　　1 2 1 2
　　8
　　1 2 3 4 1 2 3 4
　　5
　　5 4 3 3 5
　　8
　　1 2 3 4 1 3 2 4

Sample Output

　　0
　　0
　　0
　　1

HINT

　　n <= 44

Solution

　　首先，答案显然只和几个区域的连通状态有关，那么我们可以写出四种本质不同的方案。（即下图中被线分开的六块）。

　　

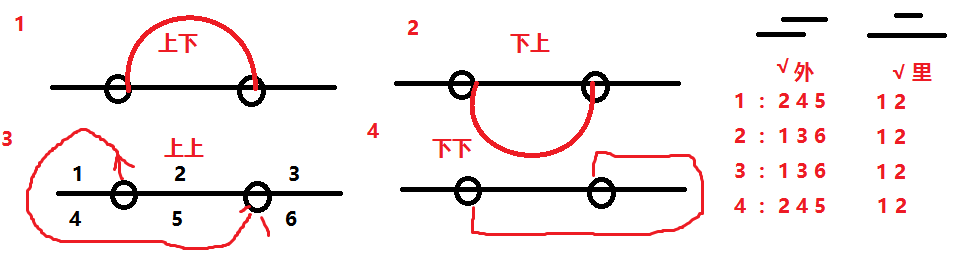
　　我们可以考虑，对于一条线，其他线（显然仅有 部分相交 与 完全相交 两种）造成的贡献。打出表来，上图是不会造成交点的线段种类。

　　既然知道了这个，我们的复杂度显然可以做到 O(4 ^ (n / 2))。还是不足以通过，怎么办呢？

　　模拟退火大法好！

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<ctime>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const int INF = ;

 int get()
 {
         int res = , Q = ; char c;
         while( (c = getchar()) <  || c > )
             if(c == '-') Q = -;
         if(Q) res = c - ;
         while( (c = getchar()) >=  && c <= )
             res = res *  + c - ;
         return res * Q;
 }

 int n, num;
 int pos[ONE], val[ONE];
 int vis[ONE], a[ONE];
 int Ans = INF;
 struct power {int l, r;} A[ONE];

 int x[ONE][ONE], y[ONE][ONE];

 void Deal_first()
 {
         x[][] = x[][] = x[][] = ;
         x[][] = x[][] = x[][] = ;
         x[][] = x[][] = x[][] = ;
         x[][] = x[][] = x[][] = ;
         for(int i = ; i <= ; i++) y[i][] = y[i][] = ;
 }

 int Now;

 int Judge(int pos, int type)
 {
         int res = Now;
         for(int i = pos, j = pos + ; j <= num; j++)
         {
             if(A[i].r < A[j].l) continue;
             if(A[i].r < A[j].r) res -= !x[a[i]][a[j]];
             if(A[j].r < A[i].r) res -= !y[a[i]][a[j]];
         }
         for(int i = , j = pos; i < pos; i++)
         {
             if(A[i].r < A[j].l) continue;
             if(A[i].r < A[j].r) res -= !x[a[i]][a[j]];
             if(A[j].r < A[i].r) res -= !y[a[i]][a[j]];
         }

         a[pos] = type;

         for(int i = pos, j = pos + ; j <= num; j++)
         {
             if(A[i].r < A[j].l) continue;
             if(A[i].r < A[j].r) res += !x[a[i]][a[j]];
             if(A[j].r < A[i].r) res += !y[a[i]][a[j]];
         }
         for(int i = , j = pos; i < pos; i++)
         {
             if(A[i].r < A[j].l) continue;
             if(A[i].r < A[j].r) res += !x[a[i]][a[j]];
             if(A[j].r < A[i].r) res += !y[a[i]][a[j]];
         }

         Now = res, Ans = min(Ans, res);
         return res;
 }

 double Random() {return (double)rand() / RAND_MAX;}
 void SA()
 {
         if(num == ) return;
         double T = num * ;
         while(T >= 0.01)
         {
             int pos = rand() % num + , type = rand() %  + ;
             int ori = Now, ori_type = a[pos];

             int dE = Judge(pos, type) - ori;
             if(dE <=  || Random() <= exp(-dE / T)) a[pos] = type;
             else Judge(pos, ori_type);

             T *= 0.9993;
         }
 }

 void Deal()
 {
         Ans = INF;
         n = get();
         for(int i = ; i <= n; i++) a[i] = get(), pos[a[i]] = vis[a[i]] = ;
         for(int i = n; i >= ; i--)
             if(!pos[a[i]]) pos[a[i]] = i;

         num = ;
         for(int i = ; i <= n; i++)
             if(!vis[a[i]] && pos[a[i]] != i)
                 A[++num] = (power){i, pos[a[i]]}, vis[a[i]] = ;

         for(int i = ; i <= num; i++)
             a[i] = rand() %  + ;
         Ans = ;
         for(int i = ; i <= num; i++)
             for(int j = i + ; j <= num; j++)
             {
                 if(A[i].r < A[j].l) break;
                 if(A[i].r < A[j].r) Ans += !x[a[i]][a[j]];
                 if(A[j].r < A[i].r) Ans += !y[a[i]][a[j]];
             }
         Now = Ans;
         for(int i = ; i <= ; i++)
             SA();
         printf("%d\n", Ans);
 }

 int main()
 {
         Deal_first();
         int T = get();
         while(T--)
             Deal();
 }