洛谷 P1852 [国家集训队]跳跳棋 解题报告

P1852 [国家集训队]跳跳棋

题目描述

跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。

我们用跳跳棋来做一个简单的游戏：棋盘上有3颗棋子，分别在\(a\)，\(b\)，\(c\)这三个位置。我们要通过最少的跳动把他们的位置移动成\(x\)，\(y\)，\(z\)。（棋子是没有区别的）

跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。

写一个程序，首先判断是否可以完成任务。如果可以，输出最少需要的跳动次数。

输入输出格式

输入格式：

第一行包含三个整数，表示当前棋子的位置\(a\) \(b\) \(c\)。（互不相同）

第二行包含三个整数，表示目标位置\(x\) \(y\) \(z\)。（互不相同）

输出格式：

如果无解，输出一行\(NO\)。

如果可以到达，第一行输出\(YES\)，第二行输出最少步数。

说明

20% 输入整数的绝对值均不超过10

40% 输入整数的绝对值均不超过10000

100% 绝对值不超过10^9

---

精巧的建模题。

划重点了划重点了一次只允许跳过1颗棋子，这句话是解题的关键。

手玩一下跳法，现有描述位置的递增三元组\((x,y,z)\)，研究它能够在一步之内跳到何处。

首先，中间的元素可以随意往两边跳到达状态\((2x-y,x,z)\)和状态\((x,z,2z-y)\)，注意到这两个三元组的边界是扩大了的。

对于两边的元素，设\(d1=y-x,d2=z-y\)

若\(d1>d2\)，则\(c\)可以往内跳，到达状态\((x,b-d2,b)\)

若\(d2>d1\)，同理。

注意到这次到达的状态三元组的边界是缩小了的，且跳法具有唯一性

若\(d1=d2\)，则边界没法缩小了，假定为边界条件。

对缩小边界的跳法具有唯一性这一性质，我们可以联想到什么呢？

将初始状态和目标状态同时缩小边界，看能否产生交集。

用树来描述这一个状态集合（树父亲的唯一性对应缩小边界的唯一性）。

到这里40分就拿到了。

---

但是我们发现，树的状态太多，无法存储。

只能每次在线询问需要的状态，复杂度为\(O(d)\)，\(d\)的两个节点的相对深度。

感觉这样就像裸奔，所以，能不能降低询问状态的复杂度呢？

再选一个三元组\((x,y,z)\)玩，现在我们只需要它缩小边界的状态了，只玩这个。

对于两边的元素，设\(d1=y-x,d2=z-y\)

只讨论\(d1>d2\)的情况，如下图

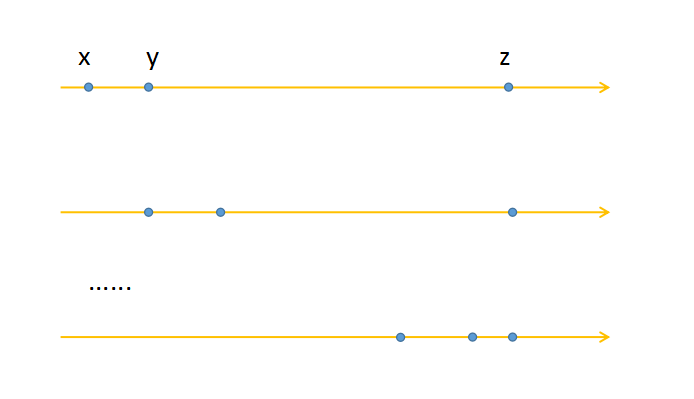
这样看，取一下模，就可以直接到达右边的状态了

当然注意一下细节，比如刚好整除的状态。

参考GCD的复杂度，单次查询差不多最坏为\(O(logD)\),\(D\)为原始给出坐标最大距离

有这个加速，我们基本就只用考虑要怎么询问状态了。

---

我们尽可能想办法只询问需要的状态。

判断是否能够到达很简单，只需要检验一下两个初始三元组的树根是否一样就行了。

如果在同一颗树了，问题就有点像LCA了。

事实上一开始的一种想法应该是直接加速的模拟往上跳，但实现起来有点困难，跳过了也不太好弄。

有一种倍增求LCA的方式是先把两个点跳到同一深度，然后两个点一起向上跳。

可以仿造这种做法先将两个状态置于一个深度，然后二分它们的LCA离它们的距离，每次加速的往上跳。

于是总复杂度：\(O(log^2D)\)

---

Code：

#include <cstdio>
#include <algorithm>
int min(int x,int y){return x<y?x:y;}
int r[3],ori[3],goa[3];
int get(int a,int b,int c)
{
    int d1=b-a,d2=c-b,cnt=0;
    if(d1>d2)
    {
        cnt=d1/d2;
        int d=d1%d2;
        if(!d)
        {
            d+=d2;
            cnt--;
        }
        cnt+=get(a,a+d,a+d+d2);
    }
    else if(d1<d2)
    {
        cnt=d2/d1;
        int d=d2%d1;
        if(!d)
        {
            d+=d1;
            cnt--;
        }
        cnt+=get(c-d-d1,c-d,c);
    }
    else
        r[0]=a,r[1]=b,r[2]=c;
    return cnt;
}
void up(int a,int b,int c,int step)
{
    if(!step)
    {
        r[0]=a,r[1]=b,r[2]=c;
        return;
    }
    int d1=b-a,d2=c-b,cnt=0;
    if(d1>d2)
    {
        cnt=d1/d2;
        int d=d1%d2;
        if(!d)
        {
            d+=d2;
            cnt--;
        }
        if(step>=cnt)
            up(a,a+d,a+d+d2,step-cnt);
        else
        {
            int k=cnt-step;
            up(a,a+d+k*d2,a+d+(k+1)*d2,0);
        }
    }
    else if(d1<d2)
    {
        cnt=d2/d1;
        int d=d2%d1;
        if(!d)
        {
            d+=d1;
            cnt--;
        }
        if(step>=cnt)
            up(c-d-d1,c-d,c,step-cnt);
        else
        {
            int k=cnt-step;
            up(c-d-(k+1)*d1,c-d-k*d1,c,0);
        }
    }
    else
        r[0]=a,r[1]=b,r[2]=c;
}
bool check(int step)
{
    int to[3];
    up(goa[0],goa[1],goa[2],step);
    to[0]=r[0];to[1]=r[1];to[2]=r[2];
    up(ori[0],ori[1],ori[2],step);
    if(to[0]!=r[0]||to[1]!=r[1]||to[2]!=r[2])
        return false;
    return true;
}
int main()
{
    int to[3],ans=0;
    scanf("%d%d%d%d%d%d",ori,ori+1,ori+2,goa,goa+1,goa+2);
    std::sort(ori,ori+3);std::sort(goa,goa+3);
    int step1=get(ori[0],ori[1],ori[2]);
    to[0]=r[0];to[1]=r[1];to[2]=r[2];
    int step2=get(goa[0],goa[1],goa[2]);
    if(to[0]!=r[0]||to[1]!=r[1]||to[2]!=r[2])
    {
        printf("NO\n");
        return 0;
    }
    if(step1<step2)
    {
        ans+=step2-step1;
        up(goa[0],goa[1],goa[2],step2-step1);
        goa[0]=r[0];goa[1]=r[1];goa[2]=r[2];
    }
    else if(step1>step2)
    {
        ans+=step1-step2;
        up(ori[0],ori[1],ori[2],step1-step2);
        ori[0]=r[0];ori[1]=r[1];ori[2]=r[2];
    }
    int l=0,rr=min(step1,step2);
    while(l<rr)
    {
        int mid=l+rr>>1;
        if(check(mid))
            rr=mid;
        else
            l=mid+1;
    }
    printf("YES\n%d\n",(l<<1)+ans);
    return 0;
}

---

2018.6.27