bzoj千题计划266：bzoj4872: [六省联考2017]分手是祝愿

http://www.lydsy.com/JudgeOnline/problem.php?id=4872

一种最优解是从大到小灯有亮的就灭掉

最优解是唯一的，且关灯的顺序没有影响

最优解对每个开关至多操作1次，（连带着的灯的亮灭改变不算）

设最优解需要操作cnt次，那么就有cnt盏灯是正确的选择

设 f[i] 表示有i种正确的选择变为有i-1种正确的选择的期望次数

那么在n盏灯中，有i盏灯操作1次就可以减少一次正确选择

有n-i盏灯是错误的选择，选了它还要把它还原，还原它也是一种正确选择，就是f[i+1]；一次错误的选择做了一次操作就是1；当然也要变成i-1种正确选择

所以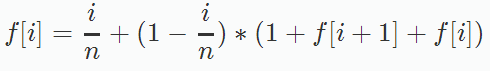

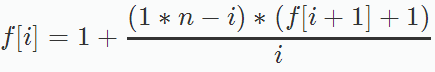
边界：f[n]=1，随便选择任何一盏灯都是正确选择

#include<cstdio>

#include<vector>

using namespace std;

#define N 100001

bool a[N];

vector<int>V[N];

int f[N],inv[N];

const int mod=;

int main()

{

    int n,k;

    scanf("%d%d",&n,&k);

    for(int i=;i<=n;++i) scanf("%d",&a[i]);

    for(int i=;i<=n;++i)

        for(int j=i;j<=n;j+=i)

            V[j].push_back(i);

    int cnt=,ans=;

    for(int i=n;i;--i)

        if(a[i])

        {

            cnt++;

            int m=V[i].size();

            for(int j=;j<m;++j) a[V[i][j]]^=;

        }

    if(cnt<=k) ans=cnt;

    else

    {

        inv[]=;

        for(int i=;i<n;++i) inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod;

        f[n]=;

        for(int i=n-;i;--i) f[i]=(+1LL*(n-i)*(+f[i+])*inv[i])%mod;

        for(int i=cnt;i>k;--i) ans=(ans+f[i])%mod;

        ans=(ans+k)%mod;

    }

    for(int i=;i<=n;++i) ans=1LL*ans*i%mod;

    printf("%d",ans);

}

4872: [Shoi2017]分手是祝愿

Time Limit: 20 Sec Memory Limit: 512 MB
Submit: 466 Solved: 304
[Submit][Status][Discuss]

Description

Zeit und Raum trennen dich und mich.

时空将你我分开。B 君在玩一个游戏，这个游戏由 n 个灯和 n 个开关组成，给定这 n 个灯的初始状态，下标为

从 1 到 n 的正整数。每个灯有两个状态亮和灭，我们用 1 来表示这个灯是亮的，用 0 表示这个灯是灭的，游戏

的目标是使所有灯都灭掉。但是当操作第 i 个开关时，所有编号为 i 的约数（包括 1 和 i）的灯的状态都会被

改变，即从亮变成灭，或者是从灭变成亮。B 君发现这个游戏很难，于是想到了这样的一个策略，每次等概率随机

操作一个开关，直到所有灯都灭掉。这个策略需要的操作次数很多， B 君想到这样的一个优化。如果当前局面，

可以通过操作小于等于 k 个开关使所有灯都灭掉，那么他将不再随机，直接选择操作次数最小的操作方法（这个

策略显然小于等于 k 步）操作这些开关。B 君想知道按照这个策略（也就是先随机操作，最后小于等于 k 步，使

用操作次数最小的操作方法）的操作次数的期望。这个期望可能很大，但是 B 君发现这个期望乘以 n 的阶乘一定

是整数，所以他只需要知道这个整数对 100003 取模之后的结果。

Input

第一行两个整数 n, k。

接下来一行 n 个整数，每个整数是 0 或者 1，其中第 i 个整数表示第 i 个灯的初始情况。

1 ≤ n ≤ 100000, 0 ≤ k ≤ n；

Output

输出一行，为操作次数的期望乘以 n 的阶乘对 100003 取模之后的结果。

Sample Input

4 0
0 0 1 1

Sample Output

512

HINT

Source

黑吉辽沪冀晋六省联考