Java 树结构的基础部分(二）

1 顺序存储二叉树

1.1 顺序存储二叉树的概念

 基本说明

从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组，

看下面的示意图。

 要求:

1) 右图的二叉树的结点，要求以数组的方式来存放 arr : [1, 2, 3, 4, 5, 6, 6]

2) 要求在遍历数组 arr 时，仍然可以以前序遍历，中序遍历和后序遍历的方式完成结点的遍历

 顺序存储二叉树的特点:

1) 顺序二叉树通常只考虑完全二叉树

2) 第 n 个元素的左子节点为 2 * n + 1

3) 第 n 个元素的右子节点为 2 * n + 2

4) 第 n 个元素的父节点为 (n-1) / 2

5) n : 表示二叉树中的第几个元素(按 0 开始编号如图所示)

 

1.2 顺序存储二叉树遍历

需求: 给你一个数组 {1,2,3,4,5,6,7}，要求以二叉树前序遍历的方式进行遍历。 前序遍历的结果应当为

1,2,4,5,3,6,7

　　代码实现

package com.lin.tree_0308;

public class ArrBinaryTreeDemo {

    public static void main(String[] args) {
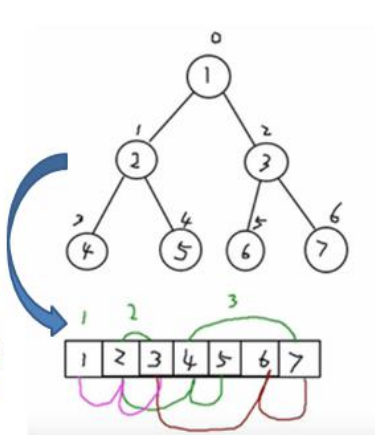
        int[] arr = {1,2,3,4,5,6,7};
        ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
        System.out.println("前序遍历：");
        arrBinaryTree.preOrder();
        System.out.println();
        System.out.println("中序遍历：");
        arrBinaryTree.infixOrder();
        System.out.println();
        System.out.println("后序遍历：");
        arrBinaryTree.postOrder();

    }
}

class ArrBinaryTree{

    private int[] arr;

    public ArrBinaryTree(int[] arr) {
        super();
        this.arr = arr;
    }

    // 重载
    public void preOrder() {
        this.preOrder(0);
    }

    public void infixOrder() {
        this.infixOrder(0);
    }

    public void postOrder() {
        this.postOrder(0);
    }

    /**
     *
     * @Description:
     * @author LinZM
     * @date 2021-3-8 19:14:45
     * @version V1.8
     * @param index 数组下标
     */
    // 前序遍历
    public void preOrder(int index) {
        if(arr == null || arr.length == 0) {
            System.out.println("数组为空！");
        }
        // 输出当前数据
        System.out.print(arr[index] + " ");
        // 向左递归
        if( ( index * 2 + 1 ) < arr.length ) {
            preOrder( index * 2 + 1 );
        }
        // 向右递归
        if( ( index * 2 +2 ) < arr.length ) {
            preOrder( index * 2 + 2 );
        }
    }

    // 中序遍历
    public void infixOrder(int index) {
        if(arr == null || arr.length == 0) {
            System.out.println("数组为空！");
        }
        // 向左递归
        if( ( index * 2 + 1 ) < arr.length) {
            infixOrder( index * 2 + 1);
        }
        // 输出当前数据
        System.out.print(arr[index] + " ");
        // 向右递归
        if( ( index * 2 + 2 ) < arr.length) {
            infixOrder(index*2 + 2);
        }
    }

    // 后序遍历
    public void postOrder(int index) {
        if(arr == null || arr.length == 0) {
            System.out.println("数组为空！");
        }
        // 向左递归
        if( ( index * 2 + 1) < arr.length ) {
            postOrder(index * 2 + 1);
        }
        // 向右递归
        if( ( index * 2 + 2 ) < arr.length) {
            postOrder(index * 2 + 2);
        }
        // 输出当前数据
        System.out.print(arr[index] + " ");
    }
}

2 线索化二叉树

2.1 先看一个问题

　　将数列 {1, 3, 6, 8, 10, 14 } 构建成一颗二叉树. n+1=7

问题分析:

1) 当我们对上面的二叉树进行中序遍历时，数列为 {8, 3, 10, 1, 6, 14 }

2) 但是 6, 8, 10, 14 这几个节点的 左右指针，并没有完全的利用上.

3) 如果我们希望充分的利用 各个节点的左右指针， 让各个节点可以指向自己的前后节点,怎么办?

4) 解决方案-线索二叉树 

 

2.2 线索二叉树基本介绍

1) n 个结点的二叉链表中含有 n+1 【公式 2n-(n-1)=n+1】 个空指针域。利用二叉链表中的空指针域，存放指向

该结点在某种遍历次序下的前驱和后继结点的指针（这种附加的指针称为"线索"）

2) 这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质

的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种

3) 一个结点的前一个结点，称为前驱结点

4) 一个结点的后一个结点，称为后继结点

 

2.3 线索二叉树应用案例 

应用案例说明：将下面的二叉树，进行中序线索二叉树。中序遍历的数列为 {8, 3, 10, 1, 14, 6}

思路分析: 中序遍历的结果：{8, 3, 10, 1, 14, 6}

 说明: 当线索化二叉树后，Node 节点的 属性 left 和 right ，有如下情况:

1) left 指向的是左子树，也可能是指向的前驱节点. 比如 ① 节点 left 指向的左子树, 而 ⑩ 节点的 left 指向的

就是前驱节点.

2) right 指向的是右子树，也可能是指向后继节点，比如 ① 节点 right 指向的是右子树，而⑩ 节点的 right 指向

的是后继节点.

 代码实现： 

package com.lin.tree_0308;

public class ThreadeBinaryTreeDemo {

    public static void main(String[] args) {
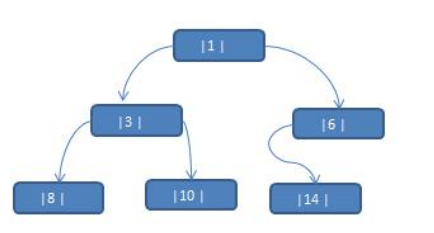
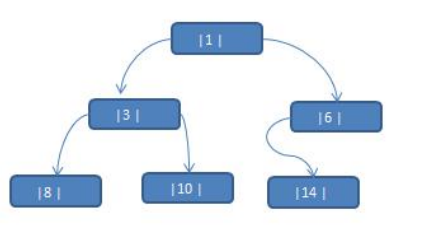
        TNode tNode1 = new TNode(1, "Tom");
        TNode tNode2 = new TNode(3, "Jack");
        TNode tNode3 = new TNode(6, "Smith");
        TNode tNode4 = new TNode(8, "Marry");
        TNode tNode5 = new TNode(10, "Linda");
        TNode tNode6 = new TNode(14, "King");

        tNode1.setLeft(tNode2);
        tNode1.setRight(tNode3);
        tNode2.setLeft(tNode4);
        tNode2.setRight(tNode5);
        tNode3.setLeft(tNode6);

        TBinaryTree tBinaryTree = new TBinaryTree();
        tBinaryTree.setRoot(tNode1);
        tBinaryTree.threadedInfixNodes(tNode1);// 10test
        TNode left = tNode5.getLeft();
        TNode right = tNode5.getRight();

        System.out.println(left);
        System.out.println(right);

//        // 中序遍历线索化二叉树
//        System.out.println("中序遍历线索化二叉树：");
//        tBinaryTree.threadedInfixList();
    }
}

class TBinaryTree{
    private TNode root;

    // 前驱节点的指针,总是保留前一个节点
    private TNode pre; 

    public void setRoot(TNode root) {
        this.root = root;
    }

    public void threadedPreNodes(TNode node) {
        if(node == null) {
            System.out.println("空！！！");
            return;
        }
        // 1 线索当前节点
        // 先处理节点的前驱节点
        if (node.getLeft() == null) {
            // 让当前节点的左指针指向前驱节点
            node.setLeft(pre);
            // 修改当前节点的左指针的类型
            node.setLeftType(1);
        }
        // 处理后继节点
        if (pre != null && pre.getRight() == null) {
            pre.setRight(node);
            pre.setRigthType(1);
        }
        // 每处理一个节点后，让当前节点是下一个节点前驱节点
        pre = node;

        threadedPreNodes(node.getLeft());

        threadedPreNodes(node.getRight());
    }

    // 二叉树中序线索化
    /**
     *
     * @Description:
     * @author LinZM
     * @date 2021-3-8 22:14:51
     * @version V1.8
     * @param node 线索化节点
     */
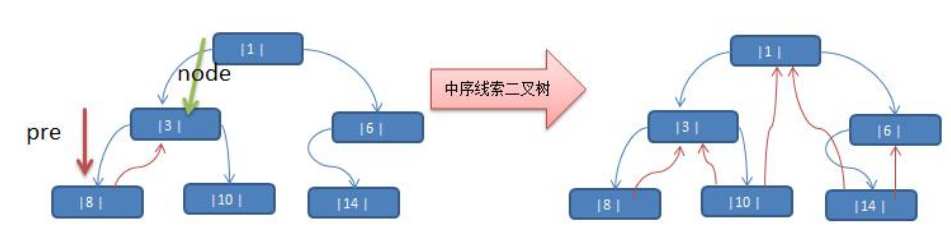
    public void threadedInfixNodes(TNode node) {
        if(node == null) {
            return;
        }

        // 1 先线索化左子树
        threadedInfixNodes(node.getLeft());
        // 2 线索化当前节点
        //     先处理节点的前驱节点
        // 节点8->节点3,一开始8为node，后面3为node
        if(node.getLeft() == null ) {
            //    让当前节点的左指针指向前驱节点
            node.setLeft(pre);
            //    修改当前节点的左指针的类型
            node.setLeftType(1);
        }
        // 处理后继节点
        if(pre != null && pre.getRight() == null) {
            pre.setRight(node);
            pre.setRigthType(1);
        }
        // 每处理一个节点后，让当前节点是下一个节点前驱节点
        // pre = 8
        pre = node;

        // 3 线索化右子树
        threadedInfixNodes(node.getRight());
    }

   // 中序遍历线索二叉树
    public void threadedInfixList() {
        // 定义一个变量，存储当前遍历的节点，从root开始
        TNode node = root;
        if(node == null) {
            System.out.println("空树！");
            return;
        }
        while(node != null) {
            // 循环找到leftType == 1 的节点，第一个找到就是8节点
            // 后面随着遍历而变化，因为当leftType == 1，说明该节点是按照线索化处理后的有效节点
            while(node.getLeftType() == 0) {
                node = node.getLeft();
            }
            // 找到8节点
            System.out.println(node);
            // 如果当前节点的右指针指向的是后继节点，就一直输出
            while(node.getRigthType() == 1) {
                node = node.getRight();
                System.out.println(node);
            }
            // 如果不是后继节点，则替换这个遍历的节点
            node = node.getRight();
        }
    }

    // 删除节点
    public void delNode(int no) {
        if (root != null) {
            // 如果只有一个root
            if (root.getNo() == no) {
                root = null;
            } else {
                root.delNode(no);
            }
        } else {
            System.out.println("空树！");
        }
    }

    // 前序遍历
    public void preOrder() {
        if(this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("二叉树为空!");
        }
    }

    // 中序遍历
    public void infixOrder() {
        if(this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("二叉树为空！");
        }
    }

    // 后序遍历
    public void postOrder() {
        if(this.root != null) {
            this.root.postOrder();
        } else {
            System.out.println("二叉树为空！");
        }
    }

    // 前序查找
    public TNode preOrderSearch(int no) {
        if(root != null) {
            return root.preOrderSearch(no);
        } else {
            return null;
        }
    }

    // 中序查找
    public TNode infixOrderSearch(int no) {
        if (root != null) {
            return root.infixOrderSearch(no);
        } else {
            return null;
        }
    }

    // 后序查找
    public TNode postOrderSearch(int no) {
        if (root != null) {
            return root.postOrderSearch(no);
        } else {
            return null;
        }
    }
}

class TNode{
    private String name;
    private int no;
    private TNode left;
    private TNode right;

    // leftType == 0 为左子树, 如果为1则表示指向前驱节点
    // rightType == 0 为右子树, 如果为1则表示指向后继节点
    private int leftType;
    private int rigthType;

    public int getLeftType() {
        return leftType;
    }

    public void setLeftType(int leftType) {
        this.leftType = leftType;
    }

    public int getRigthType() {
        return rigthType;
    }

    public void setRigthType(int rigthType) {
        this.rigthType = rigthType;
    }

    public TNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    public String getName() {
        return name;
    }
    public void setName(String name) {
        this.name = name;
    }
    public int getNo() {
        return no;
    }
    public void setNo(int no) {
        this.no = no;
    }
    public TNode getLeft() {
        return left;
    }
    public void setLeft(TNode left) {
        this.left = left;
    }
    public TNode getRight() {
        return right;
    }
    public void setRight(TNode right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "TNode [name=" + name + ", no=" + no + "]";
    }

    // 前序遍历
    public void preOrder() {
        System.out.println(this); // 输出父节点
        if(this.left != null) {
            this.left.preOrder();
        }
        if(this.right != null) {
            this.right.preOrder();
        }
    }

    // 中序遍历
    public void infixOrder() {
        if (this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this); // 输出父节点
        if (this.right != null) {
            this.right.infixOrder();
        }
    }

    // 前序遍历
    public void postOrder() {
        if (this.left != null) {
            this.left.postOrder();
        }
        if (this.right != null) {
            this.right.postOrder();
        }
        System.out.println(this); // 输出父节点
    }

    // 前序查找
    public TNode preOrderSearch(int no) {
        System.out.println("1");
        // 比较当前节点是不是
        if(this.no == no) {
            return this;
        }
        // 1 判断当前节点的左节点是否为空，如果不为空，则递归前序查找
        // 2 如果左递归前序查找，找到节点，则返回
        TNode resNode = null;
        if(this.left != null) {
            resNode = this.left.preOrderSearch(no);
        }
        if(resNode != null) {// 说明左子树找到了
            return resNode;
        }
        // 1 左递归如果没有找到，则继续判断
        // 2 当前节点的右节点是否为空，如果不为空，则继续向右递归前序查找
        if(this.right != null) {
            resNode = this.right.preOrderSearch(no);
        }
        // 这时候不管有没有找到都要返回resNode
        return resNode;
    }

    // 中序查找
    public TNode infixOrderSearch(int no) {

        TNode resNode = null;
        if(this.left != null) {
            resNode = this.left.infixOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        System.out.println("1");
        if(this.no == no) {
            return this;
        }

        if(this.right != null) {
            resNode = this.right.infixOrderSearch(no);
        }
        return resNode;
    }

    // 后序查找
    public TNode postOrderSearch(int no) {

        TNode resNode = null;
        if(this.left != null) {
            resNode = this.left.postOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }

        if(this.right != null) {
            resNode = this.right.postOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        System.out.println("1");
        if(this.no == no) {
            return this;
        }

        // 如果都没有找到
        return resNode;
    }

    /**
     *
     * @Description:1 因为我们的二叉树是单向，所以我们是判断当前节点的子节点是否需要删除节点，而不是直接去判断当前节点是否需要删除节点。<br>
     *                 2 如果当前节点的左子节点不为空，并且左子节点就是要删除节点，就将this.left = null；并且就返回（结束递归删除） <br>
     *                 3 如果当前节点的右子节点不为空，并且右子节点就是要删除节点，就将this.right = null；并且就返回（结束递归删除） <br>
     *                 4 如果第2和第3都没有删除节点，那么我们就需要向左子树进行递归删除<br>
     *                 5 如果第4补也没有删除节点，则向右子树进行递归删除<br>
     * @author LinZM
     * @date 2021-3-8 15:17:32
     * @version V1.8
     */
    public void delNode(int no) {
        if(this.left != null && this.left.no == no) {
            this.left = null;
            return;
        }

        if(this.right != null && this.right.no == no) {
            this.right = null;
            return;
        }

        if(this.left != null) {
            this.left.delNode(no);
        }

        if(this.right != null) {
            this.right.delNode(no);
        }
    }
}

 

2.4 遍历线索化二叉树

1) 说明：对前面的中序线索化的二叉树， 进行遍历

2) 分析：因为线索化后，各个结点指向有变化，因此原来的遍历方式不能使用，这时需要使用新的方式遍历

线索化二叉树，各个节点可以通过线型方式遍历，因此无需使用递归方式，这样也提高了遍历的效率。 遍历的次

序应当和中序遍历保持一致。

3) 代码： 

如上面

 

仅供参考，有错误还请指出！

有什么想法，评论区留言，互相指教指教。

觉得不错的可以点一下右边的推荐哟