跟着闫令琪老师的课程学习，总结自己学习到的知识点

课程网址GAMES101

B站课程地址GAMES101

课程资料百度网盘【提取码：0000】

计算机图形学概述

计算机图形学是一门将模型转化到屏幕上图像的一门基础学科，主要分为：Rasterization(光栅化)、Curves and Meshes(几何表示)、Ray Trancing(光线追踪)、Animation/Simulation(动画和模拟)

图形学与计算机视觉的简单界限：

(1) 计算机视觉是将屏幕上的图片转化为模型的过程;

(2) 计算机图形学是一门将模型转化到屏幕上图像的一门基础学科。

每个类别的知识框架如下图：

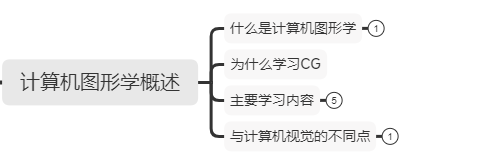
[图1]计算机图形学概述

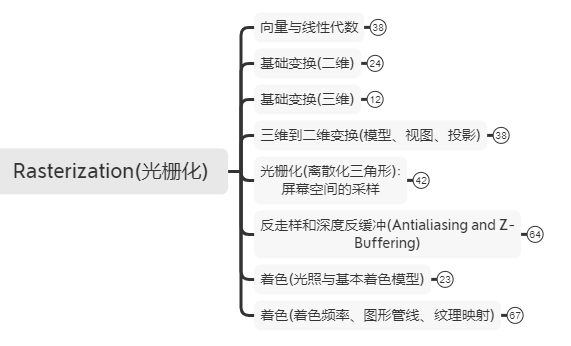
[图2]光栅化

[图3]曲线与曲面

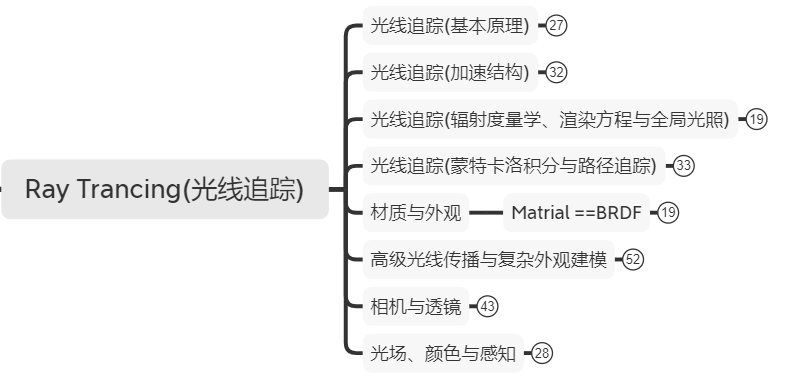
[图4]光线追踪

[图5]动画和模拟

【Notes_1】现代图形学入门——计算机图形学概述的更多相关文章

  1. [计算机图形学]绘制填充模型：重心坐标、z-buffer

    目录 一.点乘和叉乘 0. 向量表示 1. 点乘 2.叉乘 2.1 坐标运算方式 2.2 向量运算方式 2.3 叉乘的用途 二.Bounding Box 三.重心坐标 四.z-buffer 五.总结 ...

  2. 64 计算机图形学入门（1）——OpenGL环境配置与图形流水线（图像管线）

    0 引言 最近想学一下计算机图形学方面的知识,原因如下.目前本人接触了数字图像处理(opencv)以及点云处理(PCL)方面的知识,对从图像和点云中提取特征信息,并将特征转化为底层/中层语义信息有了一 ...

  3. 分享：计算机图形学期末作业！！利用WebGL的第三方库three.js写一个简单的网页版“我的世界小游戏”

    这几天一直在忙着期末考试,所以一直没有更新我的博客,今天刚把我的期末作业完成了,心情澎湃,所以晚上不管怎么样,我也要写一篇博客纪念一下我上课都没有听,还是通过强大的度娘完成了我的作业的经历.(当然作业 ...

  4. Mathematics for Computer Graphics数学在计算机图形学中的应用 [转]

    最近严重感觉到数学知识的不足! http://bbs.gameres.com/showthread.asp?threadid=10509 [译]Mathematics for Computer Gra ...

  5. 计算机图形学学习方法和相关书籍,做游戏,GIS,虚拟现实,三维引擎的都能够看看.

    本书參照<<图形学扫盲>> 整理的,原文内容引子: http://www.cppblog.com/lai3d/archive/2008/12/30/70796.html 前言: ...

  6. 计算机图形学 opengl版本 第三版------胡事民 第三章更多的绘图工具

    opengl  计算机图形学 第三版   第二部分   第三章更多的绘图工具 3.1   概述 第2章中  我们绘图使用的是屏幕窗口的基础坐标系    以像素为单位 屏幕坐标从左下角x从0延伸到scr ...

  7. 【Notes】现代图形学入门_01

    跟着闫令琪老师的课程学习,总结自己学习到的知识点 课程网址GAMES101 B站课程地址GAMES101 课程资料百度网盘[提取码:0000] 计算机图形学概述 计算机图形学是一门将模型转化到屏幕上图 ...

  8. 计算机图形学 - 图形变换（opengl版）

    作业题目: 图形变换:实现一个图形绕任意直线旋转的程序. 要求:把一个三维图形绕任意一条直线旋转,需要有初始图形,和旋转后的图形,最好也可以实时控制旋转. 最少要做出绕z轴旋转. 原理:http:// ...

  9. [图形学] 计算机图形学 with OpenGL开篇

    <计算机图形学>(第四版)正在学习中,学习目的是为了在Unity中使用shader实现不同的渲染效果. 希望在这里能把学习过程中学到的知识和遇到的问题记录下来. 工作环境是:Xcode 8 ...

随机推荐

  1. Redis命令之setbit

    setbit的作用是,对key上存储的字符串,设置或清除指定偏移量上的位(bit). 语法如下: SETBIT key offset value key是要操作的对象的键. offset是操作对象上的 ...

  2. 【uva 534】Frogger（图论--最小瓶颈路 模版题）

    题意:平面上有N个石头,给出坐标.一只青蛙从1号石头跳到2号石头,使路径上的最长便最短.输出这个值.(2≤N≤200) 解法:最小瓶颈树.而由于这题N比较小便可以用2种方法:1.最短路径中提到过的Fl ...

  3. 动态主席树【带修改】&& 例题 Dynamic Rankings ZOJ - 2112

    参考链接:https://blog.csdn.net/WilliamSun0122/article/details/77885781 一.动态主席树介绍 动态主席树与静态主席树的不同在于:静态主席树不 ...

  4. Codeforces Round #656 (Div. 3) D. a-Good String (DFS)

    题意:有一个长度为\(n=2^k\)的字符串,对于某个字符\(c\),我们定义他是一个\(c-good\),如果: ​ 1.\(len=1\),并且\(s[1]=c\). ​ 2.\(len>1 ...

  5. IIS Web API 长时间不连接后第一次访问非常缓慢

    搭建在 IIS 上的 Web API 若长时间不访问,会出现第一次访问耗时较长的现象,这与其调用应用程序池的 Idle Time-out(minutes) 即闲置超时设置有关.默认值为20,修改为0即 ...

  6. 洛谷 P4143 采集矿石 后缀数组

    题目背景 ZRQ 成功从坍塌的洞穴中逃了出来.终于,他看到了要研究的矿石.他想挑一些带回去完成任务. 题目来源:Zhang_RQ哦对了 \(ZRQ\) 就他,嗯 题目描述 ZRQ 发现这里有 \(N\ ...

  7. LINUX - pthread_mutex_lock

    原文链接:https://www.cnblogs.com/fengbohello/p/7571722.html 互斥的概念 在多线程编程中,引入了对象互斥锁的概念,来保证共享数据操作的完整性. 每个对 ...

  8. spring再学习之注解

    1.使用注解配置spring <?xml version="1.0" encoding="UTF-8"?> <beans xmlns:xsi= ...

  9. codeforces 1000C - Covered Points Count 【差分】

    题目:戳这里 题意:给出n个线段,问被1~n个线段覆盖的点分别有多少. 解题思路: 这题很容易想到排序后维护每个端点被覆盖的线段数,关键是端点值不好处理.比较好的做法是用差分的思想,把闭区间的线段改为 ...

  10. C# 类 (1)

    通常每个类都会单独定义在自己的文件里,方便区分 Class 里面定义了 变量 属性 方法 实例化这个Class,得到一个对象,然后可以使用这个对象的变量 属性和方法 属性 Properties 像是一 ...