SVM支持向量机——核函数、软间隔

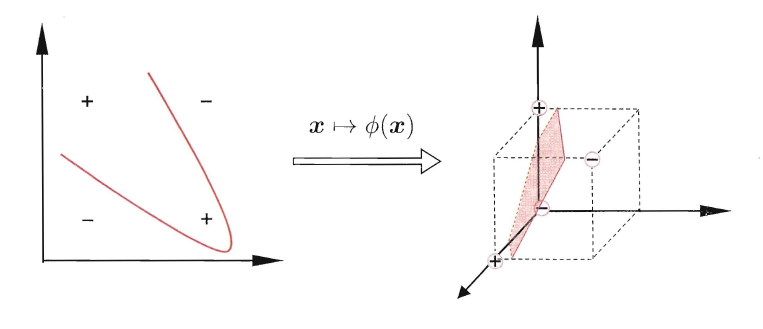
支持向量机的目的是寻找一个能讲两类样本正确分类的超平面，很多时候这些样本并不是线性分布的。

由此，可以将原始特征空间映射到更高维的特征空间，使其线性可分。而且，如果原始空间是有限维，即属性数量有限，

那么一定存在一个高维特征空间使样本可分。

k(.,.)就是核函数。整理后

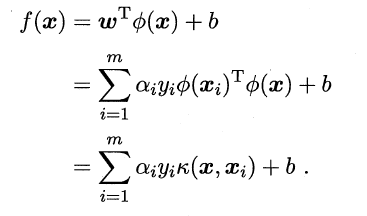
定理证明：只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。

此外，还可以组合函数得到新的核函数，比如假设K1和K2都是核函数，线性组合:r1K1+r2K2也是核函数，还有：

软间隔：

在分类问题中，我们很难完全将数据映射到一个线性可分的特征空间当中，而且即使取得了较好的分类结果，也不能确定是不是由于过拟合引起的。

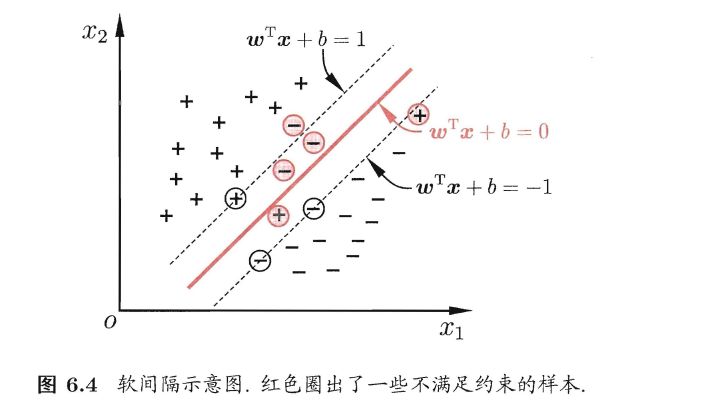
具体地，支持向量机要求所有样本都必须划分正确，这叫做“硬间隔”，而软间隔是允许一部分样本不满足约束条件的，但这样的样本要尽可能少。