龙贝格算法 MATLAB实现

龙贝格算法主要是不断递推和加速，直到满足精度要求

递推：

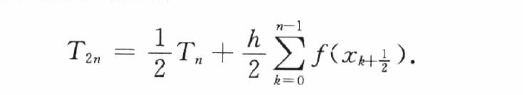
加速：

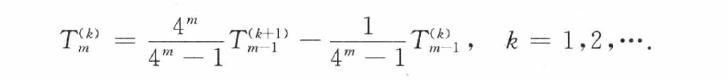
得到T表：

MATLAB代码：

function I = Romberg(f, a, b, epsilon)
    I = 0;
    h = b-a;
    k = 0;
    m = 0;
    T = zeros(5);
    %下标转换：T^(k)_0 => T(k+1,1)
    T(1,1) = h/2 * (subs(f,a) + subs(f,b));%即T^(0)_0
    delta = 2*epsilon;
    while delta > epsilon
        k = k + 1;
        h = h / 2;
        tmpSum = 0; j = a + h;
        while j < b
           tmpSum = tmpSum + subs(f, j);
           j = j + 2*h;
        end
        T(k+1, 1) = 0.5*T(k, 1) + h*tmpSum;
        j = 2;
        while j <= k+1
           T(k+1,j) = (4^(j-1)*T(k+1,j-1) - T(k, j-1)) / (4^(j-1)-1);
           j = j + 1;
        end
        delta = abs(T(k+1, k+1) - T(k, k));
    end
    I = T(k+1,k+1);
    T
end

此代码对于f(x)=xsin(x), 积分端点又是0和2pi时，计算出的T会全为零，需要把外循环条件改为 delta > epsilon | sum(T) == 0