ZOJ 3903 Ant（数学，推公示+乘法逆元）

Ant

---

Time Limit: 1 Second      Memory Limit: 32768 KB

---

There is an ant named Alice. Alice likes going hiking very much. Today, she wants to climb a cuboid. The length of cuboid's longest edge is n, and the other edges are all positive integers. Alice's starting point is a vertex of this cuboid, and she wants to arrive at the opposite vertex. The opposite vertex means the vertex which has no common planes or edges with the starting point. Just like the picture below:

Alice is very clever, she always walks on the shortest path. But she can only walk on the surface of the cuboid. Now, Alice only knows the length of cuboid's longest edge is n, and doesn't know the length of other edges. Suppose the L is the length of shortest path of a cuboid. Alice wants to compute the sum of L² for every possible cuboid.

Input

The first line of input contains an integer T(T ≤ 100) . T is the number of the cases. In the following T lines, there are a positive integer n(1≤n≤10¹⁴) in each line. n is the longest edge of the cuboid.

Output

For each test case, output the sum of L² for every possible cuboid in a line. L is the length of shortest path of a cuboid. It may be very large, so you must output the answer modulo 1000000007.

Sample Input

2
3
4

Sample Output

160
440

Hint

(3,2,1) and (3,1,2) are regrad as the same cuboids.

来自 <http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3903>

【题意】：

已知一长方体的最大边长 N

求所有可能情况下，两对顶角沿表面的最短距离（展开成平面即可）的平方和。

【解题思路】：

若长方体边长为 N A B，则 L^2 = N^2 + (A+B)^2；

即找出所有小于N的A B组合，求出平方和

例如N=3；则有组合

（1，1）（1，2）（1，3）

（2，2）（2，3）

（3，3）

即最终答案中共有 N(N+1)/2 个 N^2；

再考虑  (A+B)^2 的和：

A取值1~N，对于每个A，B取值为x~n；

将 (A+B)^2展开为 A^2+B^2+2AB 求和

其中平方项每个出现 n+1 次,

而2AB项通过代数可得

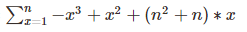
将上述项依次求和即可，由于取模原因，除法要先求逆元，这里拓展欧几里得易求。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #define LL long long
 #define mod 1000000007
 #define IN freopen("in.txt","r",stdin);
 using namespace std;

 LL x,y,gcd;
 void ex_gcd(LL a,LL b)
 {
     if(!b) {x=;y=;gcd=a;}
     else {ex_gcd(b,a%b);LL temp=x;x=y;y=temp-a/b*y;}
 }

 int main(int argc, char const *argv[])
 {
     //IN;

     LL two,six;
     ex_gcd(, mod);
     while(x<) {x+=mod;y-=;}
     two = x;
     ex_gcd(, mod);
     while(x<) {x+=mod;y-=;}
     six = x;

     int t;scanf("%d",&t);
     while(t--)
     {
         LL n, ans = ;
         scanf("%lld",&n);n%=mod;

         ans = (((((n*n)%mod)*((n*(n+))%mod))%mod)*two)%mod;
         ans = (ans + ((((((((n+)*n)%mod)*(n+))%mod)*((*n)%mod+))%mod)*six)%mod)%mod;
         ans = (ans + ((((n*n)%mod+n)%mod)*(((((n+)*n)%mod)*two)%mod))%mod)%mod;
         LL tmp = (((n*(n+))%mod)*two)%mod;
         ans = ((ans - ((tmp*tmp)%mod))%mod+mod)%mod;

         printf("%lld\n", ans%mod);
     }

     return ;
 }