对于二叉查找树的每个节点Node，它的左子树中所有的关键字都小于Node的关键字，而右子树中的所有关键字都大于Node的关键字。

二叉查找树的平均深度是O(log N)。

1.初始化

  1. class BinarySearchTree(object):
  2.     def __init__(self,key):
  3.         self.key=key
  4.         self.left=None
  5.         self.right=None

2.Find

  1.     def find(self,x):
  2.         if x==self.key:
  3.             return self
  4.         elif x<self.key and self.left:
  5.             return self.left.find(x)
  6.         elif x>self.key and self.right:
  7.             return self.right.find(x)
  8.         else:
  9.             return None

3.FindMin和FindMax

分别返回树中的最小元素与最大元素的位置。FindMin，从根开始并且只要有左儿子就向左进行查找，终止点是最小元素。FindMax则向右进行。

  1.     def findMin(self):
  2.         if self.left:
  3.             return self.left.findMin()
  4.         else:
  5.             return self
  6.     def findMax(self):
  7.         tree=self
  8.         if tree:
  9.             while tree.right:
  10.                 tree=tree.right
  11.         return tree

4.Insert

为了将x插入到树Tree中，先用find查找，如果找到x，则什么也不做。否则，将x插入到遍历路径的最后一点。

来自《Problem Solving with Algorithms and Data Structures》的图片：

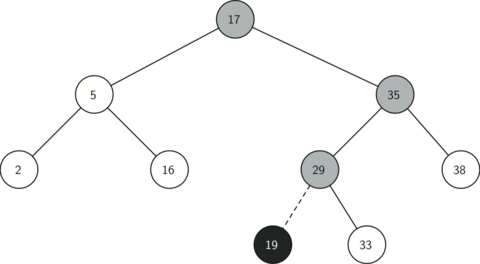
  1.     def insert(self,x):
  2.         if x<self.key:
  3.             if self.left:
  4.                 self.left.insert(x)
  5.             else:
  6.                 tree=BinarySearchTree(x)
  7.                 self.left=tree
  8.         elif x>self.key:
  9.             if self.right:
  10.                 self.right.insert(x)
  11.             else:
  12.                 tree=BinarySearchTree(x)
  13.                 self.right=tree

5.Delete

删除某节点有3种情况：

5.1 如果节点是一片树叶，那么可以立即被删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：

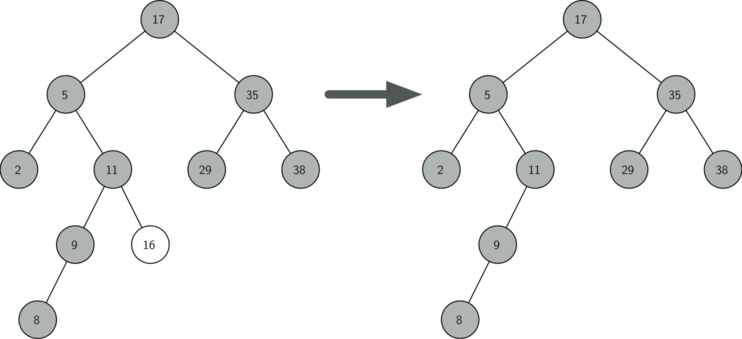
5.2 如果节点只有一个儿子，则将此节点parent的指针指向此节点的儿子，然后删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：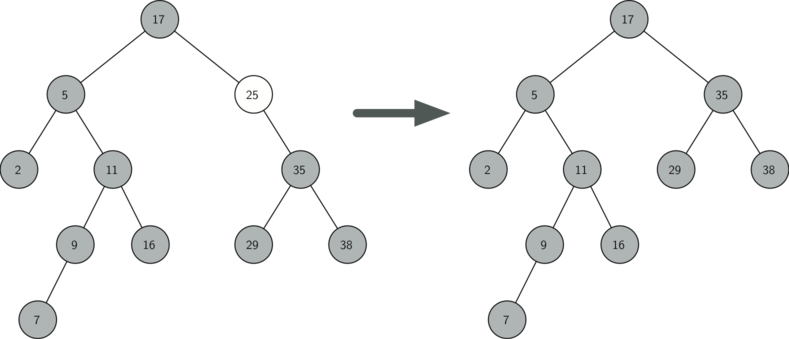

5.3 如果节点有两个儿子，则将其右子树的最小数据代替此节点的数据，并将其右子树的最小数据（不可能有左儿子，只有一个右儿子）删除。

来自《Problem Solving with Algorithms and Data Structures》的图片：

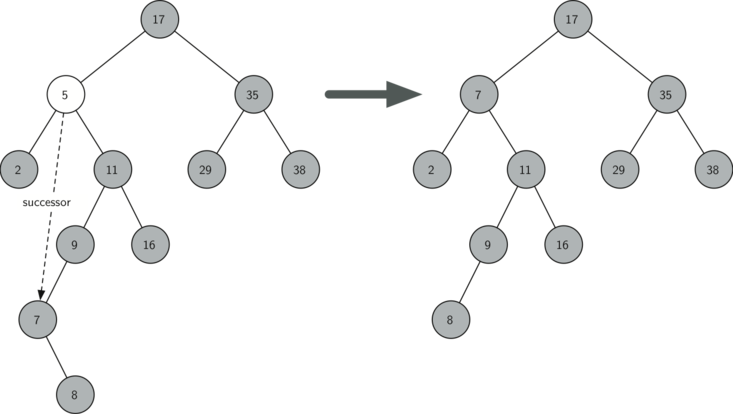
  1.     def delete(self,x):
  2.         if self.find(x):
  3.             if x<self.key:
  4.                 self.left=self.left.delete(x)
  5.                 return self
  6.             elif x>self.key:
  7.                 self.right=self.right.delete(x)
  8.                 return self
  9.             elif self.left and self.right:
  10.                 key=self.right.findMin().key
  11.                 self.key=key
  12.                 self.right=self.right.delete(key)
  13.                 return self
  14.             else:
  15.                 if self.left:
  16.                     return self.left
  17.                 else:
  18.                     return self.right
  19.         else:
  20.             return self

全部代码

  1. class BinarySearchTree(object):
  2.     def __init__(self,key):
  3.         self.key=key
  4.         self.left=None
  5.         self.right=None
  6.     def find(self,x):
  7.         if x==self.key:
  8.             return self
  9.         elif x<self.key and self.left:
  10.             return self.left.find(x)
  11.         elif x>self.key and self.right:
  12.             return self.right.find(x)
  13.         else:
  14.             return None
  15.     def findMin(self):
  16.         if self.left:
  17.             return self.left.findMin()
  18.         else:
  19.             return self
  20.     def findMax(self):
  21.         tree=self
  22.         if tree:
  23.             while tree.right:
  24.                 tree=tree.right
  25.         return tree
  26.     def insert(self,x):
  27.         if x<self.key:
  28.             if self.left:
  29.                 self.left.insert(x)
  30.             else:
  31.                 tree=BinarySearchTree(x)
  32.                 self.left=tree
  33.         elif x>self.key:
  34.             if self.right:
  35.                 self.right.insert(x)
  36.             else:
  37.                 tree=BinarySearchTree(x)
  38.                 self.right=tree
  39.     def delete(self,x):
  40.         if self.find(x):
  41.             if x<self.key:
  42.                 self.left=self.left.delete(x)
  43.                 return self
  44.             elif x>self.key:
  45.                 self.right=self.right.delete(x)
  46.                 return self
  47.             elif self.left and self.right:
  48.                 key=self.right.findMin().key
  49.                 self.key=key
  50.                 self.right=self.right.delete(key)
  51.                 return self
  52.             else:
  53.                 if self.left:
  54.                     return self.left
  55.                 else:
  56.                     return self.right
  57.         else:
  58.             return self

上述写法的缺点是很难处理空树的情况。

另一种类似于链表的写法

  1. class TreeNode(object):
  2.     def __init__(self,key,left=None,right=None,parent=None):
  3.         self.key=key
  4.         self.left=left
  5.         self.right=right
  6.         self.parent=parent
  7.     def hasLeftChild(self):
  8.         return self.left
  9.     def hasRightChild(self):
  10.         return self.right
  11.     def isLeftChild(self):
  12.         return self.parent and self.parent.left==self
  13.     def isRightChild(self):
  14.         return self.parent and self.parent.right==self
  15. class BSTree(object):
  16.     def __init__(self):
  17.         self.root=None
  18.         self.size=0
  19.     def length(self):
  20.         return self.size
  21.     def insert(self,x):
  22.         node=TreeNode(x)
  23.         if not self.root:
  24.             self.root=node
  25.             self.size+=1
  26.         else:
  27.             currentNode=self.root
  28.             while True:
  29.                 if x<currentNode.key:
  30.                     if currentNode.left:
  31.                         currentNode=currentNode.left
  32.                     else:
  33.                         currentNode.left=node
  34.                         node.parent=currentNode
  35.                         self.size+=1
  36.                         break
  37.                 elif x>currentNode.key:
  38.                     if currentNode.right:
  39.                         currentNode=currentNode.right
  40.                     else:
  41.                         currentNode.right=node
  42.                         node.parent=currentNode
  43.                         self.size+=1
  44.                         break
  45.                 else:
  46.                     break
  47.  
  48.     def find(self,key):
  49.         if self.root:
  50.             res=self._find(key,self.root)
  51.             if res:
  52.                 return res
  53.             else:
  54.                 return None
  55.         else:
  56.             return None
  57.     def _find(self,key,node):
  58.         if not node:
  59.             return None
  60.         elif node.key==key:
  61.             return node
  62.         elif key<node.key:
  63.             return self._find(key,node.left)
  64.         else:
  65.             return self._find(key,node.right)
  66.     def findMin(self):
  67.         if self.root:
  68.             current=self.root
  69.             while current.left:
  70.                 current=current.left
  71.             return current
  72.         else:
  73.             return None
  74.     def _findMin(self,node):
  75.         if node:
  76.             current=node
  77.             while current.left:
  78.                 current=current.left
  79.             return current
  80.     def findMax(self):
  81.         if self.root:
  82.             current=self.root
  83.             while current.right:
  84.                 current=current.right
  85.             return current
  86.         else:
  87.             return None
  88.     def delete(self,key):
  89.         if self.size>1:
  90.             nodeToRemove=self.find(key)
  91.             if nodeToRemove:
  92.                 self.remove(nodeToRemove)
  93.                 self.size-=1
  94.             else:
  95.                 raise KeyError,'Error, key not in tree'
  96.         elif self.size==1 and self.root.key==key:
  97.             self.root=None
  98.             self.size-=1
  99.         else:
  100.             raise KeyError('Error, key not in tree')
  101.     def remove(self,node):
  102.         if not node.left and not node.right:   #node为树叶
  103.             if node==node.parent.left:
  104.                 node.parent.left=None
  105.             else:
  106.                 node.parent.right=None
  107.  
  108.         elif node.left and node.right:   #有两个儿子
  109.             minNode=self._findMin(node.right)
  110.             node.key=minNode.key
  111.             self.remove(minNode)
  112.  
  113.         else:    #有一个儿子
  114.             if node.hasLeftChild():
  115.                 if node.isLeftChild():
  116.                     node.left.parent=node.parent
  117.                     node.parent.left=node.left
  118.                 elif node.isRightChild():
  119.                     node.left.parent=node.parent
  120.                     node.parent.right=node.left
  121.                 else:    #node为根
  122.                     self.root=node.left
  123.                     node.left.parent=None
  124.                     node.left=None
  125.             else:
  126.                 if node.isLeftChild():
  127.                     node.right.parent=node.parent
  128.                     node.parent.left=node.right
  129.                 elif node.isRightChild():
  130.                     node.right.parent=node.parent
  131.                     node.parent.right=node.right
  132.                 else:   #node为根
  133.                     self.root=node.right
  134.                     node.right.parent=None
  135.                     node.right=None

　　

　

Python数据结构————二叉查找树的实现的更多相关文章

  1. python数据结构树和二叉树简介

    一.树的定义 树形结构是一类重要的非线性结构.树形结构是结点之间有分支,并具有层次关系的结构.它非常类似于自然界中的树.树的递归定义:树(Tree)是n(n≥0)个结点的有限集T,T为空时称为空树,否 ...

  2. python数据结构与算法

    最近忙着准备各种笔试的东西,主要看什么数据结构啊,算法啦,balahbalah啊,以前一直就没看过这些,就挑了本简单的<啊哈算法>入门,不过里面的数据结构和算法都是用C语言写的,而自己对p ...

  3. python数据结构与算法——链表

    具体的数据结构可以参考下面的这两篇博客: python 数据结构之单链表的实现: http://www.cnblogs.com/yupeng/p/3413763.html python 数据结构之双向 ...

  4. python数据结构之图的实现

    python数据结构之图的实现,官方有一篇文章介绍,http://www.python.org/doc/essays/graphs.html 下面简要的介绍下: 比如有这么一张图: A -> B ...

  5. Python数据结构与算法--List和Dictionaries

    Lists 当实现 list 的数据结构的时候Python 的设计者有很多的选择. 每一个选择都有可能影响着 list 操作执行的快慢. 当然他们也试图优化一些不常见的操作. 但是当权衡的时候,它们还 ...

  6. Python数据结构与算法--算法分析

    在计算机科学中,算法分析(Analysis of algorithm)是分析执行一个给定算法需要消耗的计算资源数量(例如计算时间,存储器使用等)的过程.算法的效率或复杂度在理论上表示为一个函数.其定义 ...

  7. Python数据结构与循环语句

    # Python数据结构与循环语句:   首先编程是一项技能,类似跑步,期初不必在意细节,能使用起来就行,等学的游刃有余了再回过头来关注细节问题也不迟.  关于买书: 学会python之后,才需要买书 ...

  8. python数据结构之栈与队列

    python数据结构之栈与队列 用list实现堆栈stack 堆栈:后进先出 如何进?用append 如何出?用pop() >>> >>> stack = [3, ...

  9. python数据结构之树和二叉树(先序遍历、中序遍历和后序遍历)

    python数据结构之树和二叉树(先序遍历.中序遍历和后序遍历) 树 树是\(n\)(\(n\ge 0\))个结点的有限集.在任意一棵非空树中,有且只有一个根结点. 二叉树是有限个元素的集合,该集合或 ...

随机推荐

  1. iOS之duplicate symbols for architecture x86_64错误

    在我们写代码过程中可能会经常遇到这样一个错误: <span style="font-size:32px;color:#ff0000;">ld: 4 duplicate  ...

  2. Log4Net(三)之记录日志到数据库

    前面两篇短文向大家介绍了如何使用log4net,以及如何将log4net记录到文本文件中.下面本文将向大家介绍如何将log4net记录到数据库中. 经过前面的介绍,我想大家对使用log4net的过程已 ...

  3. [设计模式]<<设计模式之禅>>关于依赖倒置原则

    依赖倒置原则(Dependence Inversion Principle,DIP)这个名字看着有点别扭,“依赖”还“倒置”,这到底是什么意思?依赖倒置原则的原始定义是 High level modu ...

  4. JAVA基础之理解JNI原理

    JNI是JAVA标准平台中的一个重要功能,它弥补了JAVA的与平台无关这一重大优点的不足,在JAVA实现跨平台的同时,也能与其它语言(如C.C++)的动态库进行交互,给其它语言发挥优势的机会. 有了J ...

  5. Ubuntu声音消失

    声音图标是 X 将sound的Mute的勾去掉就有声音了. 参考文献: Ubuntu声音全部消失 使用的工具: Shutter

  6. Jersey(1.19.1) - Client API, Ease of use and reusing JAX-RS artifacts

    Since a resource is represented as a Java type it makes it easy to configure, pass around and inject ...

  7. JS定位PDF页码。

    由于项目中的PDF文章段落标题有些是英文,对其翻译后需要定位到具体的页码. 查询相关资料及进行尝试后发现可以用如下方法可以实现 function gotoPage(page) {            ...

  8. HDOJ2001计算两点间的距离

    计算两点间的距离 Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)Total Su ...

  9. Mysql增加主键或者更改表的列为主键的sql语句

                                                                                                        ...

  10. Unity 5.4大赞：HTC Vive经典The lab渲染器开源

    HTC Vive提供了一个不错的免费VR demo,最近1周仔细体验了一番. 仔细看了其安装文件,竟然是Unity 5.4beta版本(通过查log,知道Valve公司用的是最新的5.4.0b11版本 ...