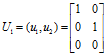SVD总结
1.概述
我们先从实数域R开始说起,再延伸到复数域C上去,先列出一个表格,把实数域以及复数域中常见的矩阵及其性质概括如下:
表1 常见矩阵及其性质

我们知道实对称矩阵正交相似于对角阵,从而将一个方阵对角化,那么一个 的矩阵能否对角化为对角阵呢,答案是肯定的,这也是奇异值分解(singular value decomposition,SVD)的意义所在。
的矩阵能否对角化为对角阵呢,答案是肯定的,这也是奇异值分解(singular value decomposition,SVD)的意义所在。
设A是一个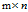 矩阵,则存在m阶正交矩阵U和n阶正交矩阵V,满足
矩阵,则存在m阶正交矩阵U和n阶正交矩阵V,满足

其中 .习惯上,设
.习惯上,设 ,称
,称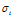 为奇异值(singular value),称U和V的前r列向量为奇异向量(singular vector),这个分解为奇异值分解。
为奇异值(singular value),称U和V的前r列向量为奇异向量(singular vector),这个分解为奇异值分解。
那现在就有疑问了,奇异值怎么求呢,m阶正交矩阵U和n阶正交矩阵V又怎么求呢,为了回答上述问题,我们将SVD写成向量形式,从而对SVD有初步的了解。令 ,
,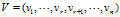 ,因为V是正交矩阵,所以有
,因为V是正交矩阵,所以有

写成向量的形式有

即
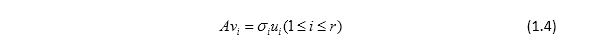
对1.1式转置得,

同理可得,

对1.4式两端左乘AT得,

将1.6式代入1.7式中,

同理可得,

故vi是实对称矩阵ATA属于 的特征向量,ui是实对称矩阵AAT属于
的特征向量,ui是实对称矩阵AAT属于 的特征向量。也就是说,奇异值就是实对称矩阵AAT(或者ATA)非零特征值的模长(即非零特征值开根号),而正交矩阵U(V)就是AAT(ATA)特征值所对应的特征向量。当然并不是随意地取m个特征向量组成U,随意地取n个特征向量组成V就可以构成A奇异值分解的正交矩阵的,U和V之间是配对的,有固定的关系,用表达式表示即为
的特征向量。也就是说,奇异值就是实对称矩阵AAT(或者ATA)非零特征值的模长(即非零特征值开根号),而正交矩阵U(V)就是AAT(ATA)特征值所对应的特征向量。当然并不是随意地取m个特征向量组成U,随意地取n个特征向量组成V就可以构成A奇异值分解的正交矩阵的,U和V之间是配对的,有固定的关系,用表达式表示即为
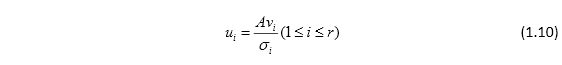
这个式子的推导在后面会介绍,现在继续探讨实对称矩阵AAT和 ATA特征值 的性质,有如下两个性质:
的性质,有如下两个性质:
1)AAT和 ATA的特征值为非负数;
|
证明: 设
故 |
2)AAT和ATA的非零特征值集合相同;
|
证明: 假设A的秩为r,因为r(AAT) = r(AT),r(ATA) = r(A),且r(A) = r(AT),故 r(AAT) = r(ATA) = r(A) = r 因为AAT是实对称矩阵,所以 设
所以 |
因此,AAT和 ATA的特征值为非负数,且AAT和 ATA的非零特征值集合相同,即求A的奇异值时,只需求出AAT和ATA其中一个矩阵的特征值即可。
接下来,推导正交矩阵U和正交矩阵V之间的配对关系,设为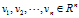 是n阶对称方阵ATA的单位正交特征向量,
是n阶对称方阵ATA的单位正交特征向量,

注意到 ,故
,故 ,即
,即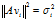 .令
.令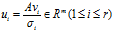 ,则
,则

且有

故 是AAT的单位正交特征向量。也就是说,当
是AAT的单位正交特征向量。也就是说,当 是ATA的单位正交特征向量时,
是ATA的单位正交特征向量时,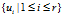 是AAT的单位正交特征向量,且
是AAT的单位正交特征向量,且 .
.
至此,矩阵A的奇异值分解就可以求出来了,首先求出AAT(ATA)的特征值,其中,非零特征值就是矩阵A的奇异值;接着求出AAT(ATA)特征值所对应的特征向量(包括零特征值对应的特征向量)作为正交矩阵U(V);最后根据配对关系求出另一个正交矩阵V(U)非零特征值所对应的特征向量,而正交矩阵V(U)的零特征值对应的特征向量则可以代入特征方程求出(或者其他方法),从而,得到任意矩阵A的奇异值分解。
这是实数域R的情况,复数域C中的奇异值分解大同小异。
设 ,
, 是A的r个奇异值,则存在m阶酉矩阵U和n阶酉矩阵V,满足
是A的r个奇异值,则存在m阶酉矩阵U和n阶酉矩阵V,满足

则上面的分解称为奇异值分解(复数域中)。
求任意一个复矩阵A的奇异值分解跟实矩阵A的奇异值分解步骤是一样的,就是非零特征值对应的次酉矩阵U1、V1的配对关系变为

其中, ,这是在求一个复矩阵A的奇异值分解时应该注意的。
,这是在求一个复矩阵A的奇异值分解时应该注意的。
2.例子
求矩阵

的奇异值分解表达式。
|
解: 步骤一:求出AAH和AHA的非零特征值(A的奇异值)
AAH的特征多项式为
AAH的特征值为 所以A的奇异值为 步骤二:求出AAH和AHA非零特征值对应的次酉矩阵U1和V1 AAH特征值为4的单位特征向量为
AAH特征值为1的单位特征向量为
所以AAH非零特征值对应的次酉矩阵U1为
因此,AHA非零特征值对应的次酉矩阵V1为
所以
|
3.应用
奇异值分解(SVD)的应用有特征降维(feature reduction)、图像压缩以及潜在语义分析(latent semantic indexing,LSI)等。就图像压缩来说,例如一张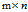 的图像,需要
的图像,需要 的矩阵来存储它。而利用奇异值分解,则只需存储矩阵的奇异值
的矩阵来存储它。而利用奇异值分解,则只需存储矩阵的奇异值 ,奇异向量
,奇异向量 和
和 ,数目为
,数目为 ,而不是
,而不是 。通常
。通常 ,所以
,所以 ,即存储该图像所需的存储量减小了。比值
,即存储该图像所需的存储量减小了。比值 称为图像的压缩比,其倒数称为数据压缩率。如果矩阵的奇异值从一个数开始值远小于前面的奇异值,则可以删去,这样在保证图像不失真的前提下,进一步减小了存储量。
称为图像的压缩比,其倒数称为数据压缩率。如果矩阵的奇异值从一个数开始值远小于前面的奇异值,则可以删去,这样在保证图像不失真的前提下,进一步减小了存储量。
SVD总结的更多相关文章
- 奇异值分解(SVD)原理与在降维中的应用
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...
- SVD奇异值分解的基本原理和运用
SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...
- 奇异值分解 SVD
一基本知识 A是一个m*n的矩阵,那么A的SVD分解为\(A_{mn} = U_{mm}\Sigma _{mn}V^T_{nn}\),其中\(U^TU = I\),\(V^TV = I\),UV的列向 ...
- SVD的几何意义,以及在去噪,推荐系统中的应用
很多文章说到奇异值分解的时候总是大概罗列下它的功能,并没有对功能及物理意义进行过多的阐述,现在我来对奇异值进行整理一下. 一 奇异值分解 对任意的矩阵A∈Fmn,rank(A)=r(矩阵的秩),总可以 ...
- Matrix Factorization SVD 矩阵分解
Today we have learned the Matrix Factorization, and I want to record my study notes. Some kownledge ...
- PCA本质和SVD
一.一些概念 线性相关:其中一个向量可以由其他向量线性表出. 线性无关:其中一个向量不可以由其他向量线性表出,或者另一种说法是找不到一个X不等于0,能够使得AX=0.如果对于一个矩阵A来说它的列是线性 ...
- 协同过滤和简单SVD优化
协同过滤(collaborative filtering) 推荐系统: 百度百科的定义是:它是利用电子商务网站向客户提供商品信息和建议,帮助用户决定应该购买什么产品,模拟销售人员帮助客户完成购买过程主 ...
- 奇异值分解(SVD)和简单图像压缩
SVD(Singular Value Decomposition,奇异值分解) 算法优缺点: 优点:简化数据,去除噪声,提高算法结果 缺点:数据的转换可能难于理解 适用数据类型:数值型数据 算法思想: ...
- 数值分析之奇异值分解(SVD)篇
在很多线性代数问题中,如果我们首先思考若做SVD,情况将会怎样,那么问题可能会得到更好的理解[1]. --Lloyd N. ...
- paper 128:奇异值分解(SVD) --- 线性变换几何意义[转]
PS:一直以来对SVD分解似懂非懂,此文为译文,原文以细致的分析+大量的可视化图形演示了SVD的几何意义.能在有限的篇幅把这个问题讲解的如此清晰,实属不易.原文举了一个简单的图像处理问题,简单形象,真 ...
随机推荐
- 在Excel中导入文本文件(CSV/TXT),自定义隔离符号
经常需要在Excel中导入文本文件,但是需要自定义隔离符号,例如空格或者逗号,参考一下方法:
- EF按时间范围条件查询
查询今日数据 db.Table.Where(d => System.Data.Entity.DbFunctions.DiffDays(d.Time, DateTime.Now) == )
- .NET中的异常处理机制(一)
1.异常处理的总体指导思想 学习C#中的异常处理机制,大概要了解以下几点: 首先,我们需要知道的事所有具体异常都是继承自System.Exception基类的. 其次,要熟悉FCL类库内置好的一些异常 ...
- AppDomain.CurrentDomain.BaseDirectory项目目录相关操作
链接:https://www.cnblogs.com/guolianyu/p/3980971.html 经常用到,每次都百度,所以自己备份一下!
- leetcode 56 合并区间 JAVA
题目: 给出一个区间的集合,请合并所有重叠的区间. 示例 1: 输入: [[1,3],[2,6],[8,10],[15,18]] 输出: [[1,6],[8,10],[15,18]] 解释: 区间 [ ...
- [CISCO] 思科交换机基本配置
思科交换机基本配置 交换机是局域网中最重要的设备,交换机是基于 MAC 来进行工作的.和路由器类似,交换 机也有 IOS,IOS 的基本使用方法是一样的.本章将简单介绍交换机的一些基本配置,以及交换 ...
- Class文件分析
java源码和class文件 源码: package classloader; public class TestCase { private int value; public int test() ...
- trunc 函数用法
转载至:http://blog.csdn.net/aqszhuaihuai/article/details/6303686 1.trunc用于日期,可精确到年,月和日. select trunc(sy ...
- c++之函数形参和实参
c++之函数形参和实参讲解 1.非地址型参数 在c++中实现模块化编程时,我们形成会遇到对自定义的函数模块传入参数的操作,即形参.这里主要讲解一个非地址型的形参. 不多说,先看代码: #include ...
- 钩子编程(HOOK) 屏蔽全部按键、鼠标及系统功能键 (4)
摘要:上篇文章<钩子编程(HOOK) 安装系统全局钩子>已经具体的解说了全局钩子的安装.本文将增强一下钩子的功能.实现屏蔽全部按键鼠标与系统功能键.要实现这个功能.须要安装两个全局钩子,& ...

 ,则
,则 ,即
,即
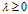 .同理可得AAT的特征值也全为非负数。
.同理可得AAT的特征值也全为非负数。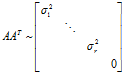 ,其中
,其中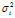 是AAT的特征值,所以有#{AAT非零特征值} = r,同理有,#{ATA非零特征值} = r.
是AAT的特征值,所以有#{AAT非零特征值} = r,同理有,#{ATA非零特征值} = r.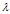 是ATA的非零特征值,即
是ATA的非零特征值,即 ,使得
,使得 ,则有
,则有
 也是AAT的非零特征值,反之亦然。故AAT和ATA具有相同的非零特征值。
也是AAT的非零特征值,反之亦然。故AAT和ATA具有相同的非零特征值。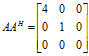 ,
,
 ,
, ,0
,0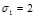 ,
, .
.