1948 NOI 嘉年华

1948 NOI 嘉年华

2011年NOI全国竞赛

 时间限制: 1 s

 空间限制: 256000 KB

 题目等级 : 大师 Master

题解

 查看运行结果

 

 

题目描述 Description

NOI2011 在吉林大学开始啦！为了迎接来自全国各地最优秀的信息学选手， 吉林大学决定举办两场盛大的 NOI 嘉年华活动，分在两个不同的地点举办。每 个嘉年华可能包含很多个活动，而每个活动只能在一个嘉年华中举办。 现在嘉年华活动的组织者小安一共收到了 n 个活动的举办申请，其中第 i 个 活动的起始时间为 Si，活动的持续时间为 Ti。这些活动都可以安排到任意一个嘉 年华的会场，也可以不安排。 小安通过广泛的调查发现，如果某个时刻，两个嘉年华会场同时有活动在进 行（不包括活动的开始瞬间和结束瞬间），那么有的选手就会纠结于到底去哪个 会场，从而变得不开心。所以，为了避免这样不开心的事情发生，小安要求不能 有两个活动在两个会场同时进行（同一会场内的活动可以任意进行）。 另外，可以想象，如果某一个嘉年华会场的活动太少，那么这个嘉年华的吸 引力就会不足，容易导致场面冷清。所以小安希望通过合理的安排，使得活动相 对较少的嘉年华的活动数量最大。 此外，有一些活动非常有意义，小安希望能举办，他希望知道，如果第 i 个 活动必须举办（可以安排在两场嘉年华中的任何一个），活动相对较少的嘉年华 的活动数量的最大值。

输入描述 Input Description

输入的第一行包含一个整数 n，表示申请的活动个数。 接下来 n 行描述所有活动，其中第 i 行包含两个整数 Si、Ti，表示第 i 个活 动从时刻 Si开始，持续 Ti的时间。

输出描述 Output Description

输出的第一行包含一个整数，表示在没有任何限制的情况下，活动较少的嘉 年华的活动数的最大值。 接下来 n 行每行一个整数，其中第 i 行的整数表示在必须选择第 i 个活动的 前提下，活动较少的嘉年华的活动数的最大值。

样例输入 Sample Input

5

8 2

1 5

5 3

3 2

5 3

样例输出 Sample Output

2

2

1

2

2

2

数据范围及提示 Data Size & Hint

【样例说明】 
在没有任何限制的情况下，最优安排可以在一个嘉年华安排活动 1, 4，而在 另一个嘉年华安排活动 3, 5，活动 2 不安排。

【数据规模与约定】 
1≤n≤200
0≤Si≤109

1≤Ti≤ 109

分类标签 Tags 点此展开

 

动态规划 单调性DP 大陆地区 NOI全国竞赛 2011年

先看这个大神的详细题解，这个写得真的很清晰很好懂啊！

　　

　　然后说说那个什么递增单凸的。

　　首先，显然pre[][x]和suf[][y]都是递减的。

　　对于x确定，y在变，f[x][y]=min(x+y,pre[i][x]+num[i][j]+suf[j][y]),显然x+y随y递增而增，pre[i][x]+num[i][j]+suf[j][y]随y递增而减。

　　

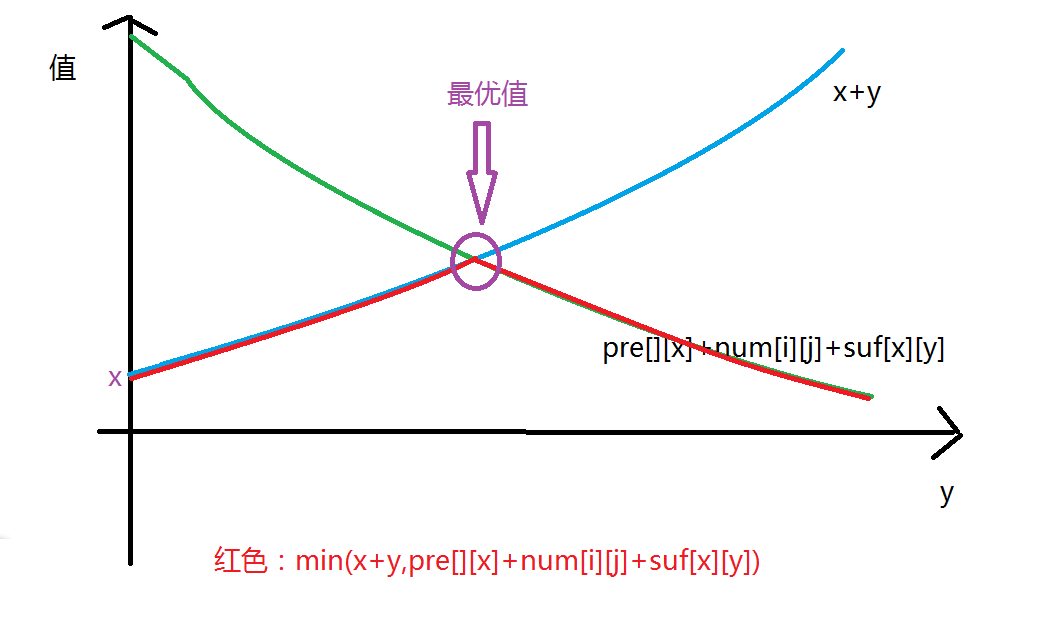
　　就是这样的，下面标红的函数就是真正的函数，显然是上凸的了。

　　所以程序里面y按顺序，找到一个now<当前最优值 就可以break了。

　　然后说明一个就是随着x的增加，取最优值的y单调递减。这个画个图也可以看出来了。

　　

　　所以就是这样做了，y这里均摊的话，就是O(n^3)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　--引自Konjakmoyu

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=;
const int inf=1e9;
int n,p,ans,s[N],t[N];
struct node{int x,y;}a[N];
int num[N][N],pre[N][N],suf[N][N];
int g[N][N];
bool cmp(const node &a,const node &b){
    return a.x<b.x;
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d%d",&s[i],&t[i]);t[i]+=s[i];
        a[i<<].x=s[i];a[i<<].y=i;
        a[i<<|].x=t[i];a[i<<|].y=-i;
    }
    sort(a+,a+n*+,cmp);
    for(int i=;i<=*n+;i++){
        if(i==||a[i].x!=a[i-].x) p++;
        if(a[i].y>) s[a[i].y]=p;
        else t[-a[i].y]=p;
    }
    for(int i=;i<=p;i++){
        for(int j=i;j<=p;j++){
            for(int k=;k<=n;k++){
                if(s[k]>=i&&t[k]<=j){
                    num[i][j]++;
                }
            }
        }
    }
    for(int i=;i<=p;i++){
        for(int j=;j<=n;j++){
            if(j>num[][i]){pre[i][j]=-inf;continue;}
            for(int k=;k<=i;k++){
                pre[i][j]=max(pre[i][j],pre[k][j]+num[k][i]);
                if(j-num[k][i]>=)     pre[i][j]=max(pre[i][j],pre[k][j-num[k][i]]);
            }
        }
    }
    for(int i=p;i>=;i--){
        for(int j=;j<=n;j++){
            if(j>num[i][p]){suf[i][j]=-inf;continue;}
            for(int k=i;k<=p;k++){
                suf[i][j]=max(suf[i][j],suf[k][j]+num[i][k]);
                if(j-num[i][k]>=)     suf[i][j]=max(suf[i][j],suf[k][j-num[i][k]]);
            }
        }
    }
    for(int i=,now,id;i<=p;i++){
        for(int j=i;j<=p;j++){
            int y=num[j][p];
            for(int x=;x<=num[][i];x++){
                for(;y>=;y--){
                    now=min(x+y,pre[i][x]+num[i][j]+suf[j][y]);
                    if(g[i][j]<=now){
                        g[i][j]=now;
                        id=y;
                    }
                    else break;
                }
                y=id;
            }
            ans=max(ans,g[i][j]);
        }
    }
    for(int i=;i<=p;i++){
        for(int j=p;j>=i;j--){
            g[i][j]=max(g[i][j],g[i][j+]);
        }
    }
    for(int i=;i<=p;i++){
        for(int j=i;j<=p;j++){
            g[i][j]=max(g[i][j],g[i-][j]);
        }
    }
    printf("%d\n",ans);
    for(int i=;i<=n;i++) printf("%d\n",g[s[i]][t[i]]);
    return ;
}