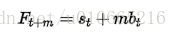Holt-Winters模型原理分析
Holt-Winters模型原理分析及代码实现(python)
引言
最近实验室老师让我去预测景区内代步车辆的投放量,于是乎,本着“一心一意地输出年富力强的劳动力”这份初心,我就屁颠屁颠地去找资料,然后发现了Holt-Winters模型 , 感觉这个模型可以有,于是就去研究一番,并总结成这篇博客了。
原理分析
移动平均(The simple moving average (SMA))
直观上,最简单的平滑时间序列的方法是实现一个无权重的移动平均,目前已知的方法是用窗口函数,平滑统计量 St就是最近k个观察值的均值。公式如下: 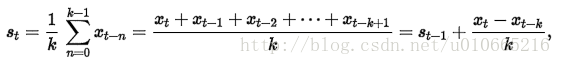
这样的方法存在明显的缺陷,当k比较小时,预测的数据平滑效果不明显,而且突出反映了数据最近的变化;当k较大时,虽然有较好的平滑效果,但是预测的数据存在延迟。而且最少需要k个值(窗口有限)。
加权移动平均
一种稍微复杂的方法是先选择一组权重因子来计算加权移动平均 
然后用这些权重来计算这些平滑统计量: 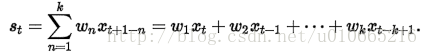
在实践中,通常在选择权重因子时,赋予时间序列中的最新数据更大的权重,并减少对旧数据的权重。这个方法也需要最少k个值,并且计算复杂。
简单指数平滑法
幸运地是有一种方法可以避免上述问题,它叫做指数平滑法。最简单的指数平滑法如下: 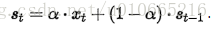
其中α是平滑因子,0 < α < 1。换句话说,平滑统计值St是当前统计值Xt与上一时间平滑值St-1的加权平均。这个简单指数平滑是很容易被应用的,因为只要有两个观察值就能计算了。这里α的选取,我们可以采用最小二乘来决定α(最小化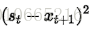
为什么被称为“指数”平滑法
从它的递推公式就能发现: 
简单指数平滑法适用于没有总体趋势的时间序列。如果用来处理有总体趋势的序列,平滑值将往往滞后于原始数据,除非α的值接近1,但这样一来就会造成不够平滑。
二次指数平滑
为了解决上述问题,于是引出了二次指数平滑,能够保留总体趋势信息。因为将指数平滑应用了两次,所以被称为二次指数平滑。与简单指数平滑相比,二次指数平滑加入了时间趋势统计量bt,公式如下: 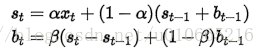
若要预测Xt后m天,公式如下:
三次指数平滑
三次指数平滑将时间序列的季节性这一特征也考虑进去了。
季节性被定义为时间序列数据的趋势,它表现出每一个周期重复自身的行为,就像任何周期函数一样。“季节”这个词用来表示行为每隔时间段L就开始自我重复。在自然界中有不同类型的季节性“累加性”(additive)和“累乘性“(multiplicative),就像加法和乘法是数学的基本运算。
如果每个12月都比每个11月多卖出1000套公寓,我们就说这样的季节趋势是“累加性”的。可以用绝对增长来表示。如果我们在夏季比冬季多卖出10%的公寓,那么季节趋势在自然中是“累乘性”的。
累乘性公式如下: 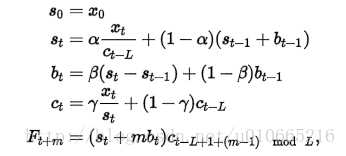
其中 α是数据平滑因子, 0 < α < 1;β是趋势平滑因子,0 < β < 1; γ是季节改变平滑因子0 < γ < 1。
初始化趋势估计b0的公式为: 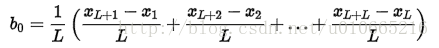
累加性公式如下: 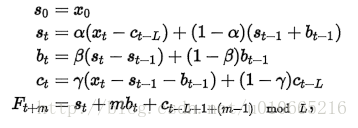
对三次指数平滑法而言,我们必须初始化一个完整的“季节”Ci的值,不过我们可以简单地设置为全1(针对累乘式)或全0(针对累加式)。只有当序列的长度较短时,我们才需要慎重考虑初始值的选取。
我们这里讲的Holt-Winters模型就是三次指数平滑法。哇,终于切入正题了。
所有的指数平滑法都要更新上一时间步长的计算结果,并使用当前时间步长的数据中包含的新信息。它们通过“混合”新信息和旧信息来实现,而相关的新旧信息的权重由一个可调整的拌和参数来控制。各种方法的不同之处在于它们跟踪的量的个数和对应的拌和参数的个数。三次指数平滑法,功能最强大,既能体现趋势性又能体现季节性,所以三次指数平滑法的参数最多,有三个。
Holt-Winters模型原理分析的更多相关文章
- jvm堆内存模型原理分析及堆内存分析工具jhat和MAT的使用超详细教程
- Android中Input型输入设备驱动原理分析(一)
转自:http://blog.csdn.net/eilianlau/article/details/6969361 话说Android中Event输入设备驱动原理分析还不如说Linux输入子系统呢,反 ...
- Mina工作原理分析
Mina是Apache社区维护的一个开源的高性能IO框架,在业界内久经考验,广为使用.Mina与后来兴起的高性能IO新贵Netty一样,都是韩国人Trustin Lee的大作,二者的设计理念是极为相似 ...
- word2vec模型原理与实现
word2vec是Google在2013年开源的一款将词表征为实数值向量的高效工具. gensim包提供了word2vec的python接口. word2vec采用了CBOW(Continuous B ...
- Android中Input型输入设备驱动原理分析<一>
话说Android中Event输入设备驱动原理分析还不如说Linux输入子系统呢,反正这个是没变的,在android的底层开发中对于Linux的基本驱动程序设计还是没变的,当然Android底层机制也 ...
- Java NIO使用及原理分析 (四)
在上一篇文章中介绍了关于缓冲区的一些细节内容,现在终于可以进入NIO中最有意思的部分非阻塞I/O.通常在进行同步I/O操作时,如果读取数据,代码会阻塞直至有 可供读取的数据.同样,写入调用将会阻塞直至 ...
- Android应用程序组件Content Provider在应用程序之间共享数据的原理分析
文章转载至CSDN社区罗升阳的安卓之旅,原文地址:http://blog.csdn.net/luoshengyang/article/details/6967204 在Android系统中,不同的应用 ...
- 消息队列NetMQ 原理分析2-IO线程和完成端口
消息队列NetMQ 原理分析2-IO线程和完成端口 前言 介绍 目的 IO线程 初始化IO线程 Proactor 启动Procator线程轮询 处理socket 获取超时时间 从完成端口获取处理完的状 ...
- java多线程系列(五)---synchronized ReentrantLock volatile Atomic 原理分析
java多线程系列(五)---synchronized ReentrantLock volatile Atomic 原理分析 前言:如有不正确的地方,还望指正. 目录 认识cpu.核心与线程 java ...
随机推荐
- ArrayList遍历的三种方式 array arrayList转换
ArrayList遍历的三种方式 - 呵呵静 - 博客园 https://www.cnblogs.com/mjyung/p/6725182.html
- sqlserver如何读写操作windows系统的文件
DECLARE @object int DECLARE @hr int DECLARE @src varchar(255), @desc varchar ...
- vue - 准备知识
一.知识 http://www.cnblogs.com/majj/https://www.cnblogs.com/majj/category/1216624.html 阮一峰 es6http://es ...
- SQL和access随机数
Access: CLng(Rnd(种子数字)*1000000) SQL Server ceiling(rand(abs(checksum(newid())))*1000000)
- 什么是虚拟DOM?
(摘抄自一篇文章,觉得这里写得非常不错,所以单独放出来,希望能对大家有帮助.)React为啥这么大?因为它实现了一个虚拟DOM(Virtual DOM).虚拟DOM是干什么的?这就要从浏览器本身讲起 ...
- "字节跳动杯"2018中国大学生程序设计竞赛-女生专场 Solution
A - 口算训练 题意:询问 $[L, R]$区间内 的所有数的乘积是否是D的倍数 思路:考虑分解质因数 显然,一个数$x > \sqrt{x} 的质因子只有一个$ 那么我们考虑将小于$\sqr ...
- Python:导入numpy报错 No module named numpy
Numpy是python的一种开源的数值计算扩展.这种工具可用来存储和处理大型矩阵,比python自身的嵌套列表结构要高效的多.但是在使用numpy时可能会出错(如上图). 解决办法:下载安装对应版本 ...
- sqlserver create table
①sql 语句创建(项目使用) use sps_db go if exists(select name from sys.tables where name='event_profile_level2 ...
- Win10取消开机密码方法
1.开始菜单输入命令“netplwiz” 2.进入到用户账户页面,选择所需账户,把“要使用本计算机,用户必须输入用户名和密码”单选框取消勾选,点击应用 3.输入密码进行 这个时候会提示输入两次该账户的 ...
- SQL学习笔记六之MySQL数据备份和pymysql模块
mysql六:数据备份.pymysql模块 阅读目录 一 IDE工具介绍 二 MySQL数据备份 三 pymysql模块 一 IDE工具介绍 生产环境还是推荐使用mysql命令行,但为了方便我们测 ...