【题解】射击-C++

Description

不难发现,豆豆能从很多事情中去思考数学,于是豆豆父母决定让他去练习射击,这是项需要集中注意力的运动,相信

能够让豆豆暂时脱离数学。学习射击的第一天就让豆豆产生 了浓厚的兴趣,射击的靶子是大饼圆,射击枪的子弹近

似圆柱,为什么要圆的不能是其他的 形状呢,于是豆豆开始构思,设计了这样一个好玩的问题:N*M 的方形格子靶子,

每个格子有两种状态凸或者凹(如下图浅色表示凹,深色表示凸)



现在用一个十字横截面的子弹(填充黑色部分)去射击,被射中的小格子凹变凸,凸变 凹,子弹放大后的横截面如下图



这种子弹最多可以覆盖 5 个格子,如图打完后,5 个格子凹凸状态发生了变化



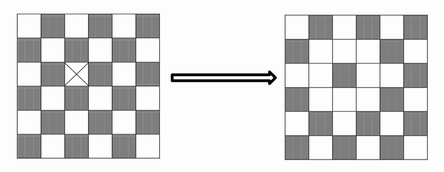
请问最少需要几次射击使靶子中所有小格子都呈现凹的状态。

注意:子弹中心点如果打到四个角上则只会影响 3 个格子,如下图黑色格子表示被子 弹中心点正好击中左上角后覆

盖的 3 个格子,如果打到除四个角的边界上,则会影响到 4 个格子,如下图右侧的 4 个黑色格子所示,这是子弹中

心点打中第 3 行第 6 列时的覆盖情 况。(也就是说子弹超出靶子部分不起效)



Input

第一行两个用空格隔开的数字 N 和 M(1<=N,M<=17)

接下来 N 行 述靶子中小格子的状态,‘X’表示凸,‘.’表示凹。

Output

输出所需要的最少射击次数

注意:输入数据保证有解

Sample Input

【样例输入 1】

5 5

XX.XX

X.X.X

.XXX.

X.X.X

XX.XX

【样例输入 2】

8 9

…XXXXX…

.X…X.

X…X.X…X

X…X

X.X…X.X

X…XXX…X

.X…X.

…XXXXX…

Sample Output

【样例输出 1】

5

【样例输出 2】

25

这道题目还是一道dfs的问题，基本上是这道题目的改版，但是在数据范围上改变了许多，如果用上一道题的方法的话连5*5的图都不能过，都需要8s多。

怎么优化呢？

我们可以不一味的列举每一个位置翻还是不翻，这样做的时间复杂度最高能达到O(n^n)，很明显，到了n≤17的范围下，这种方法肯定会炸。

为什么不通过几个简单的枚举+条件分支判断翻哪个位置呢？这样的话，就算最坏的情况，也不会耗费O(n^n)的时间复杂度。

首先，在翻棋子的基础上，写出shoot函数（也就是射击这一个位置）

void shoot(int x,int y)
{
	b[x][y]=!b[x][y];
    b[x-1][y]=!b[x-1][y];
    b[x+1][y]=!b[x+1][y];
    b[x][y-1]=!b[x][y-1];
    b[x][y+1]=!b[x][y+1];
    sum++;
}

输入的时候最好把原图转换成01矩阵，后面在dfs中直接使用双重for把01矩阵复制一份【滑稽】。

依然是dfs模板贴一下：

void dfs()//参数用来表示状态
{
    if(到达终点状态)
    {
        ...//根据题意添加
        return;
    }
    if(越界或者是不合法状态)
        return;
    if(特殊状态)//剪枝
        return ;
    for(扩展方式)
    {
        if(扩展方式所达到状态合法)
        {
            修改操作;//根据题意来添加
            标记；
            dfs（）；
            (还原标记)；
            //是否还原标记根据题意
            //如果加上（还原标记）就是 回溯法
        }
    }
}

因为这道题目的如果到达目标状态要做的事情有点多，先讲拓展。

拓展无非就是两种情况，射或者不射，如果射了，就要注意还原标记。

这部分就四行

ok[dep]=0;
dfs(dep+1);
ok[dep]=1;
//↑选↓不选
dfs(dep+1);

关键是前面、

当深度dep到了m+1（到达边界）的时候要考虑的东西有点多：

if(dep==m+1)
{
	sum=0;
    for(int i=1;i<=n;i++)
    {
    	for(int j=1;j<=m;j++)
    	{
    		b[i][j]=mp[i][j];
    	}
    }
    //复制原图
    for(int i=1;i<=m;i++)
    {
    	if(ok[i]==1)
    	{
			shoot(1,i);
		}
	}
    for(int i=2;i<=n;i++)
    {
    	for(int j=1;j<=m;j++)
    	{
    		if(b[i-1][j]==1)
    		{
				shoot(i,j);
			}
		}
	}
    f=1;
    for(int i=1;i<=m;i++)
    {
    	if(b[n][i]==1)
    	{
			f=0;
		}
	}
	if(f&&sum<ans)
	{
		ans=sum;
	}
    return;
}

自行理解（强制）

完整代码：

#include<bits/stdc++.h>
using namespace std;
char mp1[29][29];//原图
int n,m,ans=0x7f7f7f7f,sum;
int ok[29],b[29][29]/*每次dfs用来复制mp*/,mp[29][29];//01矩阵;
void shoot(int x,int y)
{
	b[x][y]=!b[x][y];
    b[x-1][y]=!b[x-1][y];
    b[x+1][y]=!b[x+1][y];
    b[x][y-1]=!b[x][y-1];
    b[x][y+1]=!b[x][y+1];
    sum++;
}
void dfs(int dep)
{
	int f;
    if(dep==m+1)
   	{
		sum=0;
	    for(int i=1;i<=n;i++)
	    {
	    	for(int j=1;j<=m;j++)
	    	{
	    		b[i][j]=mp[i][j];
	    	}
	    }
	    //复制原图
	    for(int i=1;i<=m;i++)
	    {
	    	if(ok[i]==1)
	    	{
				shoot(1,i);
			}
		}
	    for(int i=2;i<=n;i++)
	    {
	    	for(int j=1;j<=m;j++)
	    	{
	    		if(b[i-1][j]==1)
	    		{
					shoot(i,j);
				}
			}
		}
	    f=1;
	    for(int i=1;i<=m;i++)
	    {
	    	if(b[n][i]==1)
	    	{
				f=0;
			}
		}
		if(f&&sum<ans)
		{
			ans=sum;
		}
	    return;
    }
    ok[dep]=0;
    dfs(dep+1);
    ok[dep]=1;
    //↑选↓不选
    dfs(dep+1);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
    	for(int j=1;j<=m;j++)
    	{
	        cin>>mp1[i][j];
	        if(mp1[i][j]=='X')
				mp[i][j]=1;
	        else
	        	mp[i][j]=0;
    	}
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
 }

ov.