统计学习方法与Python实现（一）——感知机

统计学习方法与Python实现（一）——感知机

　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/

1、定义

　　假设输入的实例的特征空间为x属于Rⁿ的n维特征向量，输出空间为y = { +1, -1}的两点，输出的y的值表示实例的类别，则由输出空间到输出空间的函数：

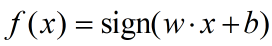
　　被称为感知机。

　　模型参数w表示内积的权值向量，b表示偏置。sign(x)为符号函数，≥0取+1，＜0取-1。

　　感知机模型的分类由线性方程 wx + b = 0 确定的分离超平面来完成，根据将特征向量代入后 wx + b 的正负来分离正、负两类。

2、学习策略

　　很明显，感知机是一种线性分类器。因此，我们为了较好的分类效果，要求数据集线性可分，也就是存在一个超平面将数据集中的两类数据完全正确的划分。

　　定义好模型后，进行学习首先要定义损失函数。

　　1、可选损失函数为误分类点的总数。但这时损失函数对参数不可导，不易优化。

　　2、可选误分类点到超平面的总距离。刻画了整个数据集上误分的程度，而且对参数可导。

　　误分类点到超平面的总距离为：

　　则损失函数为（M为误分类点的数量）：

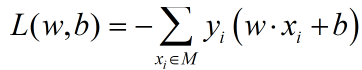
　　则优化问题转化为优化w和b的值，最小化损失函数L。选用随机梯度下降法，计算损失函数L对参数w和b的梯度。梯度的计算公式如下，也就是L分别对w和b求导。

　　可以看到，L对w的梯度为-yx，对b的梯度为-y。

　　则感知机算法的原始形式为：

　　a、任意取参数初值w0和b0得到一个初始超平面。

　　b、从数据集中选取一个样本，输入样本与标签。

　　c、检验是否有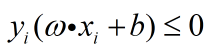。若有，则进入下一步。否则回到2。

　　d、根据梯度和选定的学习率η对参数w和b进行更新，直到误分类点被正确分类。

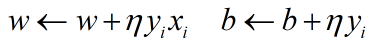
　　e、转到第b步，直到数据集中没有误分类点 或 准确率或损失函数L达到设定的阈值。得到模型。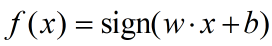

　　感知机原始算法的思想是，从数据集中挑选一个样本，对参数进行不断的更新，直到该误分样本被正确分类。

3、收敛性

　　如果数据集是线性可分的，那么一定存在一个理想超平面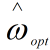使得其对数据集中的每个样本都正确分类。且该超平面满足。其中。

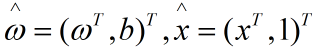　　则有：a、存在下界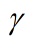，使得对于理想超平面有。

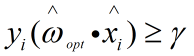　　　　　b、令R为，则感知机在数据集上的误分类次数k有上界：。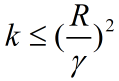

　　也就是说，对于线性可分的数据集，经过有限次搜索，总可以找到将数据集完全分开的理想超表面。具体证明主要通过相邻两次的参数更新关系和递推完成。

4、对偶形式

　　对偶形式的基本想法是，将感知机参数w和b表示为数据实例x和标签y的线性组合的形式。然后通过求解其系数而求得参数w和b。

　　根据感知机算法的原始形式可知，如果用ni表示第i个样本经过ni次参数更新，被感知机正确分类。则若记，则最后学习到的参数为：

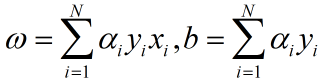
　　感知机的对偶形式算法：

　　a、将α和b的初值设为0。

　　b、从数据集中选取一个样本，输入样本与标签。

　　c、检验是否有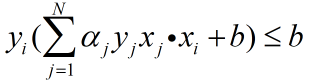，若有，则更新参数：

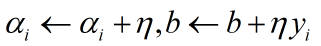
　　d、转到第b步，直到数据集中没有误分类点 或 准确率或损失函数L达到设定的阈值。得到模型。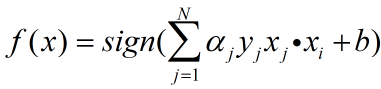

5、原始形式算法的Python实现

　　数据集选用mnist手写数字数据集，训练集60000个样本，测试集10000个样本，为0~9的手写数字，可转化为28×28的矩阵。

　　第一次先采用所有的28*28个维度的特征向量作为输入。

　　首先，第一步读入数据。用Keras来下载和读入数据，并将数据划分为‘0’和非‘0’两类。

from tensorflow.keras.datasets import mnist
import numpy as np

# 读入数据
(train_data, train_label), (test_data, test_label) = \
    mnist.load_data(r'E:\code\statistical_learning_method\Data_set\mnist.npz')

train_length = 60000
test_length = 10000

# 将’0‘的标签置为1，非’0‘的标签置为-1
train_data = train_data[:train_length].reshape(train_length, 28 * 28)
train_label = np.array(train_label, dtype='int8')
for i in range(train_length):
    if train_label[i] != 0:
        train_label[i] = 1
    else:
        train_label[i] = -1
train_label = train_label[:train_length].reshape(train_length, )

test_data = test_data[:test_length].reshape(test_length, 28 * 28)
test_label = np.array(test_label, dtype='int8')
for i in range(test_length):
    if test_label[i] != 0:
        test_label[i] = 1
    else:
        test_label[i] = -1
test_label = test_label[:test_length].reshape(test_length, )

　　第二步是初始化和编写测试函数。

# 测试模型在训练集和测试集上的准确率
def test(w, b, data, label):
    loss, acc = 0, 0
    for n in range(data.shape[0]):
        x = np.mat(data[n]).T
        y = label[n]
        L = y * (w * x + b)
        L = L[0, 0]
        if L <= 0:
            loss -= L
        else:
            acc += 1
    loss /= data.shape[0] * np.linalg.norm(w)
    acc /= data.shape[0]
    print('loss', loss, '\t', 'acc', acc, '\n')
    return loss, acc

# 初始化参数
w_init = 0.01 * np.random.random([28*28])
b_init = 0.01 * np.random.random(1)[0]
yita = 1e-9
w = np.mat(w_init)
b = b_init

　　

　　最后，对感知机模型进行训练。

for k in range(200):

    w_temp = np.mat(np.zeros(28*28)).reshape(-1, 1)
    b_temp = 0
    # 将数据集随机打乱
    rand = [i for i in range(train_length)]
    np.random.shuffle(rand)
    train_data_temp = train_data[rand]
    train_label_temp = train_label[rand]

    # 模型训练
    for index in range(train_length):
        x = np.mat(train_data_temp[index]).T
        y = train_label_temp[index]

        # 损失函数
        L = y * (w * x + b) / np.linalg.norm(w)
        L = L[0, 0]

        # 更新参数
        if L <= 0:
            w_temp += yita * x * y
            b_temp += yita * y
            w += w_temp.T
            b += b_temp
    print('time', k)

    # 在训练集和测试集上的表现
    train_loss, train_acc = test(w, b, train_data, train_label)
    test_loss, test_acc = test(w, b, test_data, test_label)

　　经过200次迭代，最后得到的结果为：

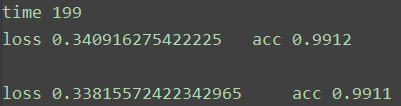
　　在60000个样本的训练集上准确率为0.9912，在10000个样本的测试集上准确率为0.9911。

6、对偶形式算法的Python实现

from tensorflow.keras.datasets import mnist
import numpy as np

(train_data, train_label), (test_data, test_label) = \
    mnist.load_data(r'E:\code\statistical_learning_method\Data_set\mnist.npz')

train_length = 1000
test_length = 1000

train_data = train_data[:train_length].reshape(train_length, 28 * 28)
train_label = np.array(train_label, dtype='int8')

for i in range(train_length):
    if train_label[i] != 0:
        train_label[i] = 1
    else:
        train_label[i] = -1
train_label = train_label[:train_length].reshape(train_length, )

test_data = test_data[:test_length].reshape(test_length, 28 * 28)
test_label = np.array(test_label, dtype='int8')
for i in range(test_length):
    if test_label[i] != 0:
        test_label[i] = 1
    else:
        test_label[i] = -1
test_label = test_label[:test_length].reshape(test_length, )

# 生成Gram矩阵
G = []
for i in range(train_length):
    G_temp = np.zeros(train_length)
    for j in range(train_length):
        G_temp[j] = np.mat(train_data[i]) * np.mat(train_data[j]).T
    G.append(G_temp)

# 计算参数w
def sigma(xj, ai):

    sum0 = 0
    for k in range(train_length):
        sum0 += ai[k] * train_label[k] * G[k][xj]
    return sum0

# 计算准确率
def acc_in_train(ai):
    acc = 0
    for t in range(train_length):
        yi = train_label[t]
        if yi * (sigma(t, ai) + b) > 0:
            acc += 1
    return acc / train_length

def acc_in_test(ai):
    acc = 0
    for t in range(test_length):
        sum1 = 0
        for xi in range(train_length):
            sum1 += ai[xi] * train_label[xi] * np.mat(train_data[xi]) * np.mat(test_data[t]).T
        yi = test_label[t]
        if yi * (sum1 + b) > 0:
            acc += 1
    return acc / test_length

a = np.zeros(train_length)
b = 0
yita = 1e-6

# 模型训练
for i in range(200000):
    rand = [i for i in range(train_length)]
    np.random.shuffle(rand)
    for j in range(train_length):
        index = rand[j]
        y = train_label[index]
        L = y * (sigma(index, a) + b)
        if L <= 0:
            a[index] += yita
            b += yita * y
            print(index, L)

    print(acc_in_train(a))

print(acc_in_test(a))

　　但是对偶形式的算法的表现并不好，训练集上准确率最高0.89，而且尝试了许多方法都没有改善。从数值上来看，原因可能是参数w太大，而每次参数更新对损失函数的影响很小。

7、其他问题

　　a、为什么在计算损失函数时，可以把w的模||w||固定为1？

　　　　因为感知机只关心损失函数的符号，不关心损失函数的大小。把w的模||w||固定为1可以使得计算简便。事实上，对于误分点到超平面的距离和的几何间隔Q=L/||w||，我们取L作为损失函数且优化使它最小，但L的极小值点不一定与Q的极小值点或||w||的极大值点相同，但感知机并不关心这个信息，只要求如果数据集线性可分，将L优化到0。这样找到的解不一定是唯一解，也不一定是最优解。但是如果要比较不同参数下的模型性能，需要计算w的模||w||，不然损失函数的值没有比较的意义。

　　b、对偶形式的优点？

　　　　因为可以事先计算训练集的内积Gram矩阵，可以使得训练的速度较快。（但是为什么表现不如原始形式？还是代码实现错了？）

参考：李航 《统计学习方法（第二版）》

　　　感知机原理小结：https://www.cnblogs.com/pinard/p/6042320.html#!comments

iwehdio的博客园：https://www.cnblogs.com/iwehdio/