HDU 1565：方格取数(1)（最大点权独立集）***

http://acm.hdu.edu.cn/showproblem.php?pid=1565

题意：中文。

思路：一个棋盘，要使得相邻的点不能同时选，问最大和是多少，这个问题就是最大点权独立集。

可以转化为所有的点权 - 最小点权覆盖集（最小割） = 最大点权独立集。

转载两个的定义：这里。

覆盖集（vertex covering set，VCS）是无向图的一个点集，使得该图中所有边都至少有一个端点在该集合内。形式化的定义是点覆盖集为G'VV∈(,)uvE∀∈，满足对于，都有 或成立，即，'uV∈'vV∈'uV∈'vV∈至少一个成立。形象地说是若干个点“覆盖”住了 与它们邻接的边，这些边恰好组成了原边集。

点独立集（vertex independent set，VIS）是无向图的一个点集，使得任两个在该集合中的点在原图中都不相邻。或者说是导出子图为零图（没有边）的点集。形式化的定义是点独立集为，满足对于，都有G'VV∈,'uvV∀∈(,)uvE∉成立。点独立集还有一种等价的定义：点独立集为，满足对于，都有'VV∈'uV∈'vV∈(,)uvE∀∈与不同时成立。

从覆盖集的定义可以看出，求覆盖集就是求最小割（最大流），这个最小点权覆盖集不是S集合就是T集合，最大权独立集就是最小点权覆盖集的补集。

因此把棋盘通过黑白染色：

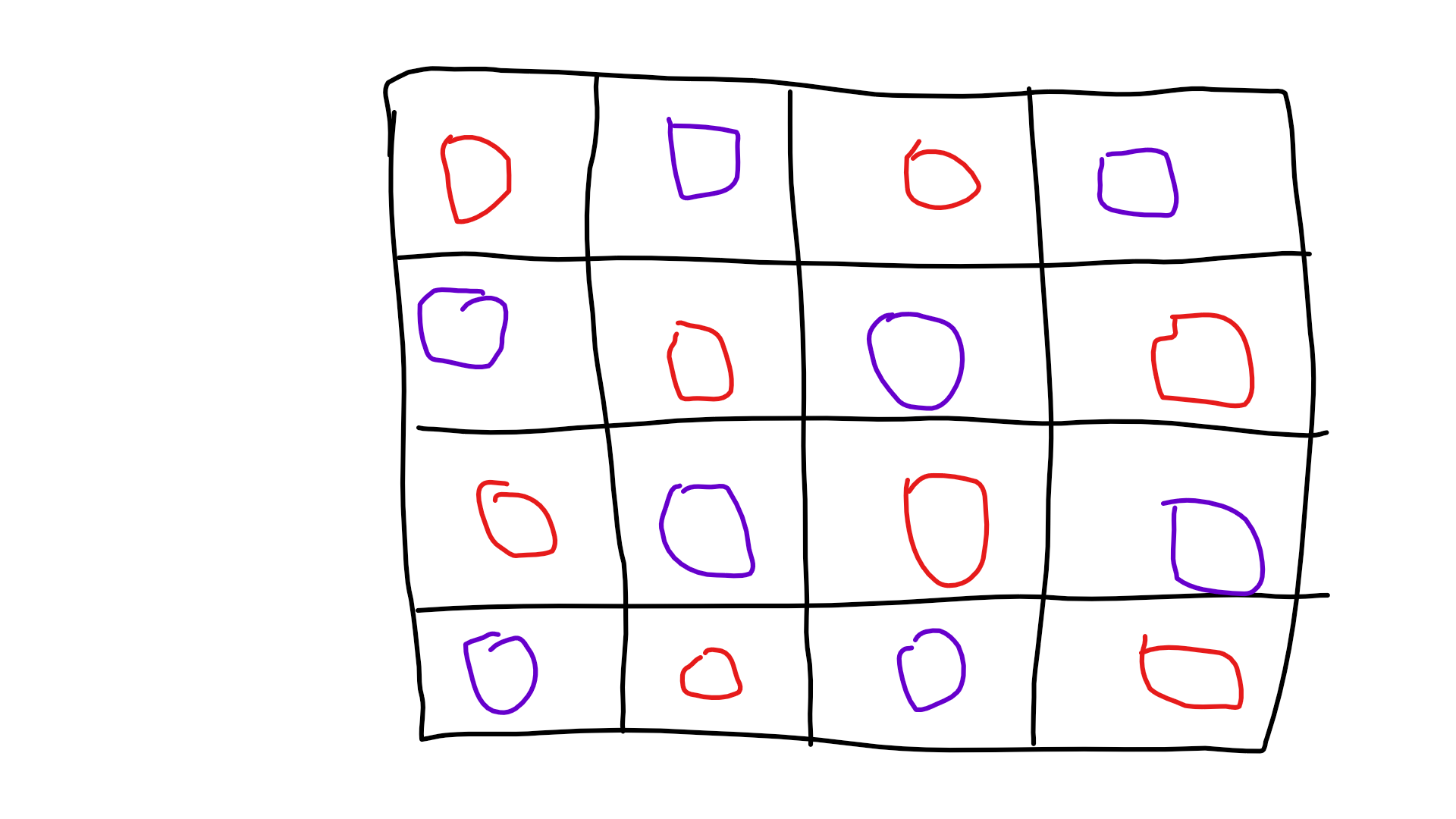
设一种颜色和S相连（容量为点权），然后用这种颜色去连接相邻另一种颜色（容量为INF），另一种颜色和T相连（容量为点权）。

 #include <cstdio>
 #include <cstring>
 #include <queue>
 using namespace std;
 #define N 510
 #define INF 0x3f3f3f3f
 typedef long long LL;
 struct Edge {
     int v, nxt, cap;
     Edge () {}
     Edge (int v, int nxt, int cap) : v(v), nxt(nxt), cap(cap) {}
 } edge[N*N];
 int head[N], tot, dis[N], cur[N], pre[N], gap[N], n, mp[][], dx[] = {, , , -}, dy[] = {, -, , };

 bool check(int x, int y) {
     if( <= x && x <= n &&  <= y && y <= n) return true;
     return false;
 }

 void Add(int u, int v, int cap) {
     edge[tot] = Edge(v, head[u], cap); head[u] = tot++;
     edge[tot] = Edge(u, head[v], ); head[v] = tot++;
 }

 int BFS(int S, int T) {
     queue<int> que; que.push(T);
     memset(dis, INF, sizeof(dis));
     memset(gap, , sizeof(gap));
     gap[]++; dis[T] = ;
     while(!que.empty()) {
         int u = que.front(); que.pop();
         for(int i = head[u]; ~i; i = edge[i].nxt) {
             int v = edge[i].v;
             if(dis[v] == INF) {
                 dis[v] = dis[u] + ;
                 gap[dis[v]]++;
                 que.push(v);
             }
         }
     }
 }

 LL ISAP(int S, int T, int n) {
     BFS(S, T);
     memcpy(cur, head, sizeof(cur));
     int u = pre[S] = S, i, index, flow; LL ans = ;
     while(dis[S] < n) {
         if(u == T) {
             flow = INF, index = S; // index = S !!!
             for(i = S; i != T; i = edge[cur[i]].v)
                 if(flow > edge[cur[i]].cap) flow = edge[cur[i]].cap, index = i;
             for(i = S; i != T; i = edge[cur[i]].v)
                 edge[cur[i]].cap -= flow, edge[cur[i]^].cap += flow;
             ans += flow, u = index;
         }
         for(i = cur[u]; ~i; i = edge[i].nxt)
             if(edge[i].cap >  && dis[edge[i].v] == dis[u] - ) break;
         if(~i) {
             pre[edge[i].v] = u; cur[u] = i; u = edge[i].v;
         } else {
             if(--gap[dis[u]] == ) break;
             int md = n;
             for(i = head[u]; ~i; i = edge[i].nxt)
                 if(md > dis[edge[i].v] && edge[i].cap > ) md = dis[edge[i].v], cur[u] = i;
             gap[dis[u] = md + ]++;
             u = pre[u];
         }
     }
     return ans;
 }

 int main() {
     while(~scanf("%d", &n)) {
         memset(head, -, sizeof(head)); tot = ;
         int S = , T = n * n + ; LL sum = ;
         for(int i = ; i <= n; i++) for(int j = ; j <= n; j++) scanf("%d", &mp[i][j]), sum += mp[i][j];
         for(int i = ; i <= n; i++) {
             for(int j = ; j <= n; j++) {
                 if((i + j) % ) Add(S, (i - ) * n + j, mp[i][j]);
                 else Add((i - ) * n + j, T, mp[i][j]);
                 for(int k = ; k < ; k++) {
                     int nx = i + dx[k], ny = j + dy[k];
                     if(check(nx, ny) && (i + j) % ) Add((i - ) * n + j, (nx - ) * n + ny, INF);
                 }
             }
         }
         printf("%lld\n", sum - ISAP(S, T, T + ));
     }
     return ;
 }

点覆盖集

（

vertex covering set

，

VCS

）是无向图

的一个点集，使得该图中所有边都至少

有一个端点在该集合内。形式化的定义是点覆盖集为

G

'

V

V

∈

(

,

)

u

v

E

∀

∈

，满足对于

，都有

或

成立，即

，

'

u

V

∈

'

v

V

∈

'

u

V

∈

'

v

V

∈

至少一个成立。形象地说是若干个点“覆盖”住了

与它们邻接的边，这些边恰好组成了原边集。

点独立集

（

vertex independent set

，

VIS

）是无向图

的一个点集，使得任两个在该集合中

的点在原图中都不相邻。或者说是导出子图为零图（没有边）的点集。形式化的定义是点独

立集为

，满足对于

，都有

G

'

V

V

∈

,

'

u

v

V

∀

∈

(

,

)

u

v

E

∉

成立。点独立集还有一种等价的定义：

点独立集为

，满足对于

，都有

'

V

V

∈

'

u

V

∈

'

v

V

∈

(

,

)

u

v

E

∀

∈

与

不同时成立。