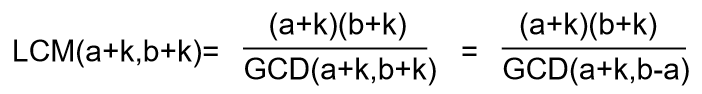Codeforces Round #554 (Div. 2) C. Neko does Maths (数论 GCD(a,b) = GCD(a,b-a))
•题意
给出两个正整数 a,b;
求解 k ,使得 LCM(a+k,b+k) 最小,如果有多个 k 使得 LCM() 最小,输出最小的k;
•思路
时隔很久,又重新做这个题
温故果然可以知新❤
重要知识点
GCD(a,b)=GCD(a,b-a)=GCD(b,b-a) (b>a)
证明:
设GCD(a,b)=c
则a%c=0,b%c=0,(b-a)%c=0
所以GCD(a,b-a)=c
得GCD(a,b)=GCD(a,b-a)
gcd(a+k,b-a)肯定是(b-a)的因子
所以gcd(a+k,b+k)是(b-a)的因子,所以我们就枚举(b-a)的因子(把因子称为i)
使得 (a+k)为i的倍数
解出k,再判断lcm是否符合最小
注意这里枚举的i只是(a+k)和(b+k)的公约数,不一定是最大公约数gcd
两者的公约数得到的是公倍数 公倍数=a*b/公约数
如果是最大公约数的话两者的公倍数一定是最小,
这里是没有甄别是否是最大公约数而是简单的得到公约数,然后得到的是公倍数
在所有的公倍数中,最小公倍数是最小的
所以并不影响解最小公倍数的答案
例如:
12 30
12 30
公约数i=1 k=1 a+k=13 b+k=31 公倍数=403
公约数i=2 k=2 a+k=14 b+k=32 公倍数=224
公约数i=3 k=3 a+k=15 b+k=33 公倍数=165
公约数i=6 k=6 a+k=18 b+k=36 公倍数=108
公约数i=9 k=6 a+k=18 b+k=36 公倍数=72
公约数i=18 k=6 a+k=18 b+k=36 公倍数=36最小公约数36,此时k=6
另外一个思路可以求最大公约数 然后求最小公倍数,看HHHyacinth的博客
•代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll a,b;
ll ans,lcm=0x3f3f3f3f3f3f3f3f;
int main()
{
cin>>a>>b;
ll d=abs(a-b);
for(ll i=;i*i<=d;i++)
{
if(d%i==)//枚举b-a的因数i
{
ll k=(i-a%i)%i;//把a凑成i的倍数需要+k
ll t=(a+k)*(b+k)/i;// a*b/i得公倍数
if(t<lcm)
{
lcm=t;
ans=k;
} ll ii=d/i;
k=(ii-a%ii)%ii;
t=(a+k)*(b+k)/ii;
if(t<lcm)
{
lcm=t;
ans=k;
}
}
}
cout<<ans<<endl;
}
Codeforces Round #554 (Div. 2) C. Neko does Maths (数论 GCD(a,b) = GCD(a,b-a))的更多相关文章
- Codeforces Round #554 (Div. 2) C.Neko does Maths (gcd的运用)
题目链接:https://codeforces.com/contest/1152/problem/C 题目大意:给定两个正整数a,b,其中(1<=a,b<=1e9),求一个正整数k(0&l ...
- Codeforces Round #554 (Div. 2) C. Neko does Maths (简单推导)
题目:http://codeforces.com/contest/1152/problem/C 题意:给你a,b, 你可以找任意一个k 算出a+k,b+k的最小公倍数,让最小公倍数尽量小,求出 ...
- Codeforces Round #554 (Div. 2) C. Neko does Maths(数学+GCD)
传送门 题意: 给出两个整数a,b: 求解使得LCM(a+k,b+k)最小的k,如果有多个k使得LCM()最小,输出最小的k: 思路: 刚开始推了好半天公式,一顿xjb乱操作: 后来,看了一下题解,看 ...
- Codeforces Round #554 (Div. 2) 1152B. Neko Performs Cat Furrier Transform
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152B. Neko Performs Cat Furrier Transform 题目链接:"ht ...
- Codeforces Round #554 (Div. 2) 1152A - Neko Finds Grapes
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152A - Neko Finds Grapes 题目链接:"https://codeforces. ...
- Codeforces Round #554 (Div. 2) B. Neko Performs Cat Furrier Transform(思维题+log2求解二进制位数的小技巧)
传送门 题意: 给出一个数x,有两个操作: ①:x ^= 2k-1; ②:x++; 每次操作都是从①开始,紧接着是② ①②操作循环进行,问经过多少步操作后,x可以变为2p-1的格式? 最多操作40次, ...
- Codeforces Round #554 (Div. 2) E Neko and Flashback (欧拉路径 邻接表实现(当前弧优化..))
就是一欧拉路径 贴出邻接表欧拉路径 CODE #include <bits/stdc++.h> using namespace std; const int MAXN = 100005; ...
- Codeforces Round #554 (Div. 2) F2. Neko Rules the Catniverse (Large Version) (矩阵快速幂 状压DP)
题意 有nnn个点,每个点只能走到编号在[1,min(n+m,1)][1,min(n+m,1)][1,min(n+m,1)]范围内的点.求路径长度恰好为kkk的简单路径(一个点最多走一次)数. 1≤n ...
- Codeforce Round #554 Div.2 C - Neko does Maths
数论 gcd 看到这个题其实知道应该是和(a+k)(b+k)/gcd(a+k,b+k)有关,但是之后推了半天,思路全无. 然而..有一个引理: gcd(a, b) = gcd(a, b - a) = ...
随机推荐
- JavaScript规定了几种语言类型?
JavaScript中的每一个值都有它自己的类型,JavaScript规定了七种语言类型: 1.Undefined 2.Null 3.Boolean 4.String 5.Number 6.Symbo ...
- 9个WebGL的演示
1. WebGL Water This incredible demo is as fluid as you could believe. Raise and drop the ball into ...
- scikit-learn杂记
1.数据预处理 二值化 import numpy as np from sklearn import preprocessing X = np.array([[1., -1., 2.], [2., 0 ...
- Java 泛型学习总结
前言 Java 5 添加了泛型,提供了编译时类型安全检测机制,该机制允许程序员在编译时检测到非法的类型. 泛型的本质是参数化类型,可以为以前处理通用对象的类和方法,指定具体的对象类型.听起来有点抽象, ...
- 洛谷 题解 UVA658 【这不是bug,而是特性 It's not a Bug, it's a Feature!】
[题意] 补丁在修正\(BUG\)时,有时也会引入新的\(BUG\),假定有\(n(n<=20)\)个潜在\(BUG\),和\(m(m<=100)\)个补丁,每个补丁用两个长度为\(n\) ...
- MyBatis从入门到精通(六):MyBatis动态Sql之if标签的用法
最近在读刘增辉老师所著的<MyBatis从入门到精通>一书,很有收获,于是将自己学习的过程以博客形式输出,如有错误,欢迎指正,如帮助到你,不胜荣幸! 本篇博客主要讲解如何使用if标签生成动 ...
- mac vim 配色
syntax on set nu set noic set t_Co=256 set tabstop=4 set nocompatible set shiftwidth=4 set softtabst ...
- html手机自适应屏幕
<meta name="viewport" content="height=device-width, initial-scale=1.0, maximum-sca ...
- scrapy 发post请求
可以使用 yield scrapy.FormRequest(url, formdata, callback)方法发送POST请求. 如果希望程序执行一开始就发送POST请求,可以重写Spider类的s ...
- C# 实现最小化托盘功能
winform程序实现最小化托盘显示 1.创建新的解决方案,解决方案名称和路径自定义 2.在解决方案下面新建一个窗体,从左边工具箱,将NotifyIcon拖过去窗体,该控件的作用是:运行程序期间在Wi ...