树和二叉树->基础知识

树的表示方法

1 一般表示法

2 广义表表示法

3 凹入表示法

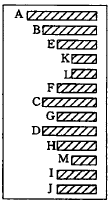
树的基本术语：

树：n(n>=0)个结点的有限集

结点：包含一个数据元素及若干指向其子树的分支

结点的度：结点拥有的子树数成为结点的度

叶子(也叫终端结点)：度为0的结点

非终端结点(也叫分支结点)：度不为0的结点

树的度：树内各结点的度的最大值

孩子：结点的子树的根成为该结点的孩子

双亲：若B结点是A结点的孩子，则A结点是B结点的双亲

堂兄弟：其双亲在同一层的结点护卫堂兄弟

结点的层次：从根开始定义起，根为第一层，根的孩子为第二层

树的深度(也叫高度)：树中结点的最大层次。

有序树：子树有序的树

无序树：不考虑子树的顺序

森林：m(m>=0)棵互不相交的树的集合。

二叉树定义

在二叉树中，每个结点至多只有两颗子树，并且，二叉树的子树有左右之分，其次序不能颠倒。关于树的术语也都适用于二叉树

完全二叉树定义

一颗深度为k，除第k层外，其它各层的结点数(1~k-1)的结点数都达到最大个数，第k层有叶子结点，且叶子结点从左至右依次排布，这就是完全二叉树。

满二叉树定义

一颗深度为k且有2^k-1个结点的二叉树成为满二叉树

二叉树性质

性质1 在二叉树的第i层上至多有2^i-1个结点

性质2 深度为k的二叉树至多有2^k-1个结点, 用等比数列求和公式就可容易证明

性质3 对任何一颗二叉树T，终端结点数n0和度为2的结点数n2的关系如下：

n0=n2+1，在博客“内部排序->选择排序->树形选择排序”的附录1已经证明过。

性质4 具有n个结点的完全二叉树的深度为[log₂n]+1

证明：假设深度为k， 根据性质2和完全二叉树的定义有

2^k-1 < n <= 2^k-1

性质5 对一颗有n个结点的完全二叉树，按层序编号，则对任一结点，都有：

(1)   根结点除外的其它结点i的双亲为[i/2]

(2)   结点i的左孩子结点为2*i，(2*i不超过树的结点个数的情况下)

(3)   结点i的右孩子结点为2*i+1, (2*i+1不超过树的结点个数的情况下)