Codeforces 438D The Child and Sequence - 线段树

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

1. Print operation l, r. Picks should write down the value of .
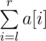2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

Can you help Picks to perform the whole sequence of operations?

Input

The first line of input contains two integer: n, m (1 ≤ n, m ≤ 10⁵). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 10⁹) — initial value of array elements.

Each of the next m lines begins with a number type .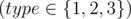

• If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
• If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 2.
• If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 3.

Output

For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

Examples

Input

5 5 1 2 3 4 5 2 3 5 4 3 3 5 1 2 5 2 1 3 3 1 1 3

Output

8 5

Input

10 10 6 9 6 7 6 1 10 10 9 5 1 3 9 2 7 10 9 2 5 10 8 1 4 7 3 3 7 2 7 9 9 1 2 4 1 6 6 1 5 9 3 1 10

Output

49 15 23 1 9

Note

Consider the first testcase:

• At first, a = {1, 2, 3, 4, 5}.
• After operation 1, a = {1, 2, 3, 0, 1}.
• After operation 2, a = {1, 2, 5, 0, 1}.
• At operation 3, 2 + 5 + 0 + 1 = 8.
• After operation 4, a = {1, 2, 2, 0, 1}.
• At operation 5, 1 + 2 + 2 = 5.

---

　　题目大意 维护一个数列，有3种操作，分别是区间求和，区间取模和单点修改。

　　显然线段树(请不要问我为什么。。。学长的Tag打在那儿的)

　　区间求和和单点修改都是线段树的拿手好戏，但是对于区间取模似乎不是那么好做。考虑可以区间批量更新sum吗？显然不行。

　　但是考虑到这里只有单点修改，而且对一个大于模数的数取模，它的值至多为它原来的值的一半。

　　所以区间记录一个最大值剪枝，每次区间取模先判断是否有必要进行递归取模，如果有，就暴力递归下去，在底层修改。

Code

 /**
  * Codeforces
  * Problem#438D
  * Accepted
  * Time: 436ms
  * Memory: 8740k
  */
 #include <bits/stdc++.h>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;

 typedef class SegTreeNode {
     public:
         int maxv;
         long long sum;
         SegTreeNode *l, *r;

         SegTreeNode():maxv(), sum(), l(NULL), r(NULL) {        }

         inline void pushUp() {
             maxv = max(l->maxv, r->maxv);
             sum = l->sum + r->sum;
         }
 }SegTreeNode;

 typedef class SegTree {
     public:
         SegTreeNode* root;

         SegTree():root(NULL) {        }
         SegTree(int n, int* a) {
             build(root, , n, a);
         }

         void build(SegTreeNode*& node, int l, int r, int* a) {
             node = new SegTreeNode();
             if(l == r) {
                 node->sum = node->maxv = a[l];
                 return;
             }
             int mid = (l + r) >> ;
             build(node->l, l, mid, a);
             build(node->r, mid + , r, a);
             node->pushUp();
         }

         void update(SegTreeNode*& node, int l, int r, int idx, int val) {
             if(l == r) {
                 node->maxv = node->sum = val;
                 return;
             }
             int mid = (l + r) >> ;
             if(idx <= mid)    update(node->l, l, mid, idx, val);
             else update(node->r, mid + , r, idx, val);
             node->pushUp();
         }

         void update(SegTreeNode*& node, int l, int r, int ql, int qr, int moder) {
             if(l == r) {
                 node->maxv = (node->sum %= moder);
                 return;
             }
             int mid = (l + r) >> ;
             if(qr <= mid && node->l->maxv >= moder)    update(node->l, l, mid, ql, qr, moder);
             else if(ql > mid && node->r->maxv >= moder)    update(node->r, mid + , r, ql, qr, moder);
             else if(qr > mid && ql <= mid) {
                 if(node->l->maxv >= moder)
                     update(node->l, l, mid, ql, mid, moder);
                 if(node->r->maxv >= moder)
                     update(node->r, mid + , r, mid + , qr, moder);
             }
             node->pushUp();
         }

         long long query(SegTreeNode*& node, int l, int r, int ql, int qr) {
             if(l == ql && r == qr) {
                 return node->sum;
             }
             int mid = (l + r) >> ;
             if(qr <= mid)    return query(node->l, l, mid, ql, qr);
             if(ql > mid)    return query(node->r, mid + , r, ql, qr);
                 return query(node->l, l, mid, ql, mid) + query(node->r, mid + , r, mid + , qr);
             }
 }SegTree;              

 int n, m;
 int* arr;
 SegTree st;
 inline void init() {
     scanf("%d%d", &n, &m);
     arr = new int[(n + )];
     for(int i = ; i <= n; i++)
         scanf("%d", arr + i);
     st = SegTree(n, arr);
 }                      

 inline void solve() {
     int opt, a, b, c;
     while(m--) {
         scanf("%d%d%d", &opt, &a, &b);
         if(opt == ) {
             printf(Auto"\n", st.query(st.root, , n, a, b));
         } else if(opt == ) {
             scanf("%d", &c);
             st.update(st.root, , n, a, b, c);
         } else {
             st.update(st.root, , n, a, b);
         }
     }
 }

 int main() {
     init();
     solve();
     return ;
 }