LSTM改善RNN梯度弥散和梯度爆炸问题

我们给定一个三个时间的RNN单元，如下：

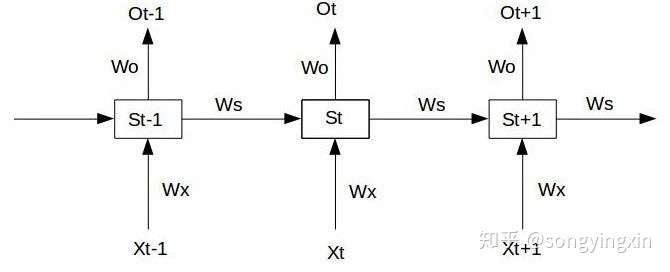
我们假设最左端的输入 $S_0$ 为给定值，且神经元中没有激活函数（便于分析），则前向过程如下：

$S_1 = W_xX_1 + W_sS_0 + b_1 \qquad \qquad \qquad O_1 = W_oS_1 + b_2 \\ S_2 = W_xX_2 + W_sS_1 + b_1 \qquad \qquad \qquad O_2 = W_oS_2 + b_2 \\ S_3 = W_xX_3 + W_sS_2 + b_1 \qquad \qquad \qquad O_3 = W_oS_3 + b_2 \\$

在 $t=3$ 时刻，损失函数为 $L_3 = \frac{1}{2}(Y_3 - O_3)^2$ ，那么如果我们要训练RNN时，实际上就是是对 $W_x, W_s, W_o,b_1,b_2$ 求偏导，并不断调整它们以使得 $L_3$ 尽可能达到最小（参见反向传播算法与梯度下降算法)。

那么我们得到以下公式：

$\frac{\delta L_3}{\delta W_0} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta W_0} \\ \frac{\delta L_3}{\delta W_x} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_x} \\ \frac{\delta L_3}{\delta W_s} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_s} \\$

将上述偏导公式与第三节中的公式比较，我们发现，随着神经网络层数的加深对 $W_0$ 而言并没有什么影响，而对 $W_x, W_s$ 会随着时间序列的拉长而产生梯度消失和梯度爆炸问题。

根据上述分析整理一下公式可得，对于任意时刻t对 $W_x, W_s$ 求偏导的公式为：

$\frac{\delta L_t}{\delta W_x } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_x} \\ \frac{\delta L_t}{\delta W_s } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_s}$

由以上可知，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

参考：

https://www.cnblogs.com/bonelee/p/10475453.html

https://www.zhihu.com/question/34878706

LSTM改善RNN梯度弥散和梯度爆炸问题的更多相关文章

RNN神经网络产生梯度消失和梯度爆炸的原因及解决方案
1.RNN模型结构循环神经网络RNN(Recurrent Neural Network)会记忆之前的信息,并利用之前的信息影响后面结点的输出.也就是说,循环神经网络的隐藏层之间的结点是有连接的,隐藏 ...
讨论LSTM和RNN梯度消失问题
1RNN为什么会有梯度消失问题 (1)沿时间反向方向:t-n时刻梯度=t时刻梯度* π(W*激活函数的导数)
Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸
Backpropagation Through Time (BPTT) 梯度消失与梯度爆炸下面的图显示的是RNN的结果以及数据前向流动方向假设有 \[ \begin{split} h_t & ...
梯度消失与梯度爆炸 ==> 如何选择随机初始权重
梯度消失与梯度爆炸当训练神经网络时,导数或坡度有时会变得非常大或非常小,甚至以指数方式变小,这加大了训练的难度这里忽略了常数项b.为了让z不会过大或者过小,思路是让w与n有关,且n越大,w应该越小 ...
梯度消失、梯度爆炸以及Kaggle房价预测
梯度消失.梯度爆炸以及Kaggle房价预测梯度消失和梯度爆炸考虑到环境因素的其他问题 Kaggle房价预测梯度消失和梯度爆炸深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸( ...
L14梯度消失、梯度爆炸
梯度消失.梯度爆炸以及Kaggle房价预测梯度消失和梯度爆炸考虑到环境因素的其他问题 Kaggle房价预测梯度消失和梯度爆炸深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸( ...
L8梯度消失、梯度爆炸
houseprices数据下载: 链接:https://pan.baidu.com/s/1-szkkAALzzJJmCLlJ1aXGQ 提取码:9n9k 梯度消失.梯度爆炸以及Kaggle房价预测代 ...
logistics回归简单应用——梯度下降，梯度上升，牛顿算法（一）
警告:本文为小白入门学习笔记由于之前写过详细的过程,所以接下来就简单描述,主要写实现中遇到的问题. 数据集是关于80人两门成绩来区分能否入学: 数据集: http://openclassroom.s ...

随机推荐

Vue 之 slot(插槽）
前言: vue中关于插槽的文档说明很短,语言又写的很凝练,再加上其和methods,data,computed等常用选项在使用频率.使用先后上的差别,这就有可能造成初次接触插槽的开发者容易产生“算了吧 ...
QPainter 提高绘制效率的方法
原文: https://my.oschina.net/u/3919756/blog/1944747 如果我们用painter一个一个的绘制直线,圆等在控件上,绘制效率会不高.为了提高效率,我们可以设置 ...
python - super 寻找继承关系
""" super 是根据当前类对象的 mro 的继承顺序进行函数的调用的 """ class Base(object): def fn(s ...
[GraphQL] Reuse GraphQL Selection Sets with Fragments
Fragments are selection sets that can be used across multiple queries. They allow you to refactor re ...
Neo4j 快速清除数据库数据
在开发过程中,很多时候需要快(简)速(单)清(粗)除(暴)Neo4j中存在的海量数据节点和关系数据.在这种情况下,delete和detach从性能上都已力不从心.Neo4j官方推荐清库方法,即删除gr ...
exam9.6&&7
emmm 改题稍紧张,以后几篇并一起写 9.6 (前十并没有参加本次考试) 于是我就rank8了一道题一道题来先说T1: 显然是一个高精度GCD,于是打算用计算器算一下时间复杂度众所周知gcd是 ...
P4316 绿豆蛙的归宿期望DP
P4316 绿豆蛙的归宿期望DP DAG上,每条边有边权,走向相连每条路的概率相等,问从起点到终点所经过的路径总长度期望因为发现终点走到终点期望为0,定义$f[i]$从终点走到$i$所经过 ...
代码 | 自适应大邻域搜索系列之(6) - 判断接受准则SimulatedAnnealing的代码解析
前言前面三篇文章对大家来说应该很简单吧?不过轻松了这么久,今天再来看点刺激的.关于判断接受准则的代码.其实,判断接受准则有很多种,效果也因代码而异.今天介绍的是模拟退火的判断接受准则.那么,相关的原 ...
TensorFlow(十六)：TensorFlow GPU准备
一:安装cuda 下载地址二:安装cuDNN 三:安装GPU版TensorFlow 注意:gpu版的TensorFlow打开tensorboard要使用:tensorboard --logdir C ...
redis基准性能测试
1 测试目的了解redis在不同情况下的性能表现,并分析其性能瓶颈,找出相应的解决方案. 2 redis基准测试概览运行下列命令可以了解自己的redis服务器的基本性能指标. 通过loopback ...

LSTM改善RNN梯度弥散和梯度爆炸问题

LSTM改善RNN梯度弥散和梯度爆炸问题的更多相关文章

随机推荐

热门专题