【基础算法-ST表】入门 -C++

前言

学了树状数组看到ST表模板跃跃欲试的时候发现完全没思路，因为给出的查询的时间实在太短了！几乎是需要完成O(1)查询。所以ST表到底是什么神仙算法能够做到这么快的查询？

ST表

ST表是一个用来解决RMQ问题（区间最值问题）的有效算法。

它的功能也很简单。

O(nlogn)预处理，O(1)查询区间最值。

其他好像真还没什么用了

算法

ST表利用的是倍增的思路来实现的。

怎么说呢，ST表确实很神奇。

拿最大值来说吧...

我们用f[i][j]表示第i个数开始的\(2^j\)个数中的最大值。

p.s. 下面的图是这个大佬画的

转移的时候我们可以把当前区间拆成两个区间并分别取最大值（注意这里的编号是从1开始的）



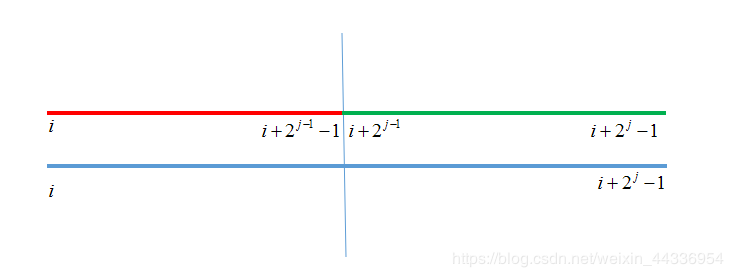
查询也比较简单；

首先要计算\(log_2\)（区间长度）

然后分别查询左右段店，保证覆盖整个区间。



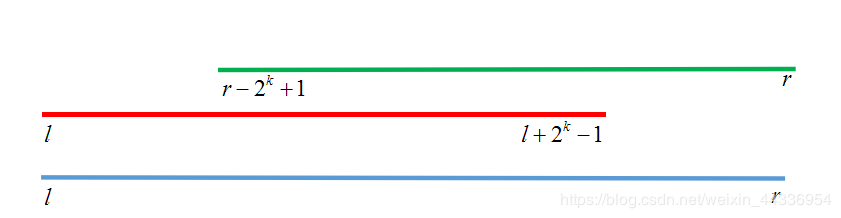
p.s因为我们需要找到一个点x使得\(x+2^k-1=r\)，然后移项就可以得到\(x=r-2^k+1\)，所以把x作为从右端点查询的区间的左端点，也就是\(r-2^k+1\)。

代码

代码就比较好理解了...

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
   int x=0,f=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){
       if(ch=='-')
           f=-1;
       ch=getchar();
   }
   while(ch>='0'&&ch<='9'){
       x=(x<<1)+(x<<3)+(ch^48);
       ch=getchar();
   }
   return x*f;
}

int f[100001][40],b,n,m,p,l,r;
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++)
    	f[i][0]=read();
    b=(int)(log(n)/log(2));
    for(int j=1;j<=b;j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    for(int i=1;i<=m;i++)
    {
        l=read(),r=read();
        p=(int)(log(r-l+1)/log(2));
        printf("%d\n",max(f[l][p],f[r-(1<<p)+1][p]));
    }
    return 0;
}

ov.